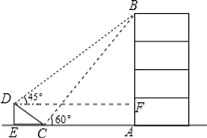
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.

(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
参考答案:
【答案】(1)2米;(2)(6+![]() )或(6-
)或(6-![]() )米.
)米.
【解析】试题分析:(1)在在Rt△DCE中,利用30°所对直角边等于斜边的一半,可求出DE=2米;(2)过点D作DF⊥AB于点F,则AF=2,根据三角函数可用BF表示BC、BD,然后可判断△BCD是Rt△,进而利用勾股定理可求得BF的长,AB的高度也可求.
试题解析:(1)在Rt△DCE中,∠DEC=90°,∠DCE=30°,∴DE=![]() DC=2米;(2)过D作DF⊥AB,交AB于点F,则AF=DE=2米.∵∠BFD=90°,∠BDF=45°,∴∠BFD=45°,∴BF=DF.设BF=DF=x米,则AB=(x+2)米,在Rt△ABC中,∠BAC=90°,∠BCA=60°,∴sin∠BCA=
DC=2米;(2)过D作DF⊥AB,交AB于点F,则AF=DE=2米.∵∠BFD=90°,∠BDF=45°,∴∠BFD=45°,∴BF=DF.设BF=DF=x米,则AB=(x+2)米,在Rt△ABC中,∠BAC=90°,∠BCA=60°,∴sin∠BCA=![]() ,∴BC=AB÷sin∠BCA=(x+2)÷
,∴BC=AB÷sin∠BCA=(x+2)÷![]() =
=![]() 米,在Rt△BDF中,∠BFD=90°,
米,在Rt△BDF中,∠BFD=90°,![]() 米,∵∠DCE=30°,∠ACB=60°,∴∠DCB=90°.∴
米,∵∠DCE=30°,∠ACB=60°,∴∠DCB=90°.∴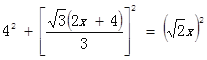 ,解得:x=4+
,解得:x=4+![]() 或x=4﹣
或x=4﹣![]() ,则AB=(6+
,则AB=(6+![]() )米或(6﹣
)米或(6﹣![]() )米.
)米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为5,圆心O到直线l的距离为4,则⊙O与直线l的位置关系为_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形OABC的边长为2,顶点A,C分别在x轴,y轴的正半轴上,点E是BC的中点,F是AB延长线上一点且FB=1.

(1)求经过点O,A,E三点的抛物线解析式;
(2)点P在抛物线上运动,当点P运动到什么位置时△OAP的面积为2,请求出点P的坐标;
(3)在抛物线上是否存在一点Q,使△AFQ是等腰直角三角形?若存在直接写出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列关于x的单项式,探究其规律:x2,3x4,5x6,7x8,9x10,11x12,…,按照上述规律,第2019个单项式是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形的内角和是
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
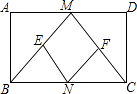
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB=时,四边形MENF是正方形(只写结论,不需证明). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD为⊙O的直径,点A是弧BC的中点,AD交BC于E点,AE=2,ED=4.

(1)求证:
 ~△ADB;
~△ADB;(2) 求
 的值;
的值; (3)延长BC至F,连接FD,使
 的面积等于
的面积等于 ,求证:DF与⊙O相切。
,求证:DF与⊙O相切。
相关试题

