【题目】【问题提出】已知∠AOB=70°,∠AOD=![]() ∠AOC,∠BOD=3∠BOC(∠BOC<45°),求∠BOC的度数.
∠AOC,∠BOD=3∠BOC(∠BOC<45°),求∠BOC的度数.
【问题思考】聪明的小明用分类讨论的方法解决.
(1)当射线OC在∠AOB的内部时,①若射线OD在∠AOC内部,如图1,可求∠BOC的度数,解答过程如下:
设∠BOC=α,∴∠BOD=3∠BOC=3α,∴∠COD=∠BOD﹣∠BOC=2α,∴∠AOD=![]() ∠AOC,
∠AOC,
∴∠AOD=∠COD=2α,∴∠AOB=∠AOD+∠BOD=2α+3α=5α=70°,∴α=14°,∴∠BOC=14°
问:当射线OC在∠AOB的内部时,②若射线OD在∠AOB外部,如图2,请你求出∠BOC的度数;
【问题延伸】(2)当射线OC在∠AOB的外部时,请你画出图形,并求∠BOC的度数.
【问题解决】综上所述:∠BOC的度数分别是 .

参考答案:
【答案】(1)②∠BOC=30°;(2)作图见解析,∠BOC的度数分别是14°,30°,10°,42°.
【解析】试题分析: (1)②由已知条件得出∠COD、∠AOD、∠AOB与∠BOC的关系,求出∠BOC的度数;
(2)分类讨论,根据∠AOD、∠BOD.∠AOB与∠BOC的关系,得出∠BOC的度数.
试题解析:
(1)②设∠BOC=α,则∠BOD=3α,若射线OD在∠AOB外部,如图2:

∠COD=∠BOD﹣∠BOC=2α,
∵∠AOD=![]() ∠AOC,
∠AOC,
∴∠AOD=![]() ∠COD=
∠COD= ![]() ,
,
∴∠AOB=∠BOD﹣∠AOD=3α﹣![]() =
= ![]() =70°,
=70°,
∴α=30°.∴∠BOC=30°;
(2)当射线OC在∠AOB外部时,根据题意,此时射线OC靠近射线OB,
∵∠BOC<45°,∠AOD=![]() ∠AOC,
∠AOC,
∴射线OD的位置也只有两种可能;
①若射线OD在∠AOB内部,如图3所示,

则∠COD=∠BOC+∠COD=4α,
∴∠AOB=∠BOD+∠AOD=3α+4α=7α=70°,
∴α=10°,
∴∠BOC=10°;
②若射线OD在∠AOB外部,如图4,

则∠COD=∠BOC+∠BOD=4α,
∵∠AOD=![]() ∠AOC,
∠AOC,
∴∠AOD=![]() ∠COD=
∠COD=![]() α,
α,
∴∠AOB=∠BOD﹣∠AOD=3α﹣![]() α=
α=![]() α=70°,
α=70°,
∴α=42°,
∴∠BOC=42°;
综上所述:∠BOC的度数分别是14°,30°,10°,42°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上A,B表示的数分别是3和﹣5,它们之间的距离可以表示为( )
A. ﹣5+3B. ﹣5﹣3C. |﹣5+3|D. |﹣5﹣3|
-
科目: 来源: 题型:
查看答案和解析>>【题目】若方程2x+1=﹣3的解是关于x的方程7﹣2(x﹣a)=3的解,则a的值为( )
A. ﹣2B. ﹣4C. ﹣5D. ﹣6
-
科目: 来源: 题型:
查看答案和解析>>【题目】
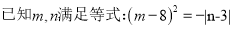
求m,n的值
已知m是关于x的方程:3x+4a=5x-4的解,求a的值;
已知线段AB=m,在直线AB上取一点P,恰好使AP=nPB,其中点Q为线段PB的中点,求线段AQ的长度。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,DE⊥AC于点E,∠EDC:∠EDA=1:3,且AC=12,则DE的长度是 (结果用根号表示).
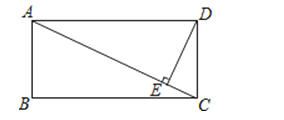
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.
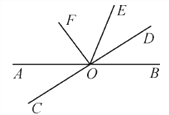
(1)判断OF与OD的位置关系;
(2)若∠AOC∶∠AOD=1∶5,求∠EOF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于函数y=﹣x+3,下列结论正确的是( )
A. 它的图象必经过点(1,1) B. 它的图象经过第一、二、三象限
C. 它的图象与y轴的交点坐标为(0,3) D. y随x的增大而增大
相关试题

