【题目】如图所示,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.
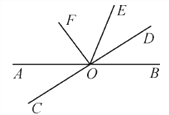
(1)判断OF与OD的位置关系;
(2)若∠AOC∶∠AOD=1∶5,求∠EOF的度数.
参考答案:
【答案】(1) OF⊥OD,理由见解析;(2) 60°.
【解析】试题分析:(1)根据角平分线的性质,可得![]() 与
与![]() 的关系,根据角的和差,可得
的关系,根据角的和差,可得![]() 的度数,可得答案;
的度数,可得答案;
(2)根据补角的性质, ![]() 可得
可得![]() 的度数,根据角的和差,可得
的度数,根据角的和差,可得![]() 的度数,根据角平分线的性质,可得答案.
的度数,根据角平分线的性质,可得答案.
试题解析:
(1)因为OF平分∠AOE,
所以∠AOF=∠EOF=![]() ∠AOE.
∠AOE.
又因为∠DOE=∠BOD=![]() ∠BOE,
∠BOE,
所以∠DOE+∠EOF=![]() (∠BOE+∠AOE)=
(∠BOE+∠AOE)= ![]() ×180°=90°,
×180°=90°,
即∠FOD=90°.
所以OF⊥OD.
(2)设∠AOC=x°,
因为∠AOC∶∠AOD=1∶5,
所以∠AOD=5x°.
因为∠AOC+∠AOD=180°,
所以x+5x=180,x=30.
所以∠DOE=∠BOD=∠AOC=30°.
又因为∠FOD=90°,
所以∠EOF=90°-30°=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
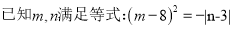
求m,n的值
已知m是关于x的方程:3x+4a=5x-4的解,求a的值;
已知线段AB=m,在直线AB上取一点P,恰好使AP=nPB,其中点Q为线段PB的中点,求线段AQ的长度。
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题提出】已知∠AOB=70°,∠AOD=
 ∠AOC,∠BOD=3∠BOC(∠BOC<45°),求∠BOC的度数.
∠AOC,∠BOD=3∠BOC(∠BOC<45°),求∠BOC的度数.【问题思考】聪明的小明用分类讨论的方法解决.
(1)当射线OC在∠AOB的内部时,①若射线OD在∠AOC内部,如图1,可求∠BOC的度数,解答过程如下:
设∠BOC=α,∴∠BOD=3∠BOC=3α,∴∠COD=∠BOD﹣∠BOC=2α,∴∠AOD=
 ∠AOC,
∠AOC,∴∠AOD=∠COD=2α,∴∠AOB=∠AOD+∠BOD=2α+3α=5α=70°,∴α=14°,∴∠BOC=14°
问:当射线OC在∠AOB的内部时,②若射线OD在∠AOB外部,如图2,请你求出∠BOC的度数;
【问题延伸】(2)当射线OC在∠AOB的外部时,请你画出图形,并求∠BOC的度数.
【问题解决】综上所述:∠BOC的度数分别是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,DE⊥AC于点E,∠EDC:∠EDA=1:3,且AC=12,则DE的长度是 (结果用根号表示).
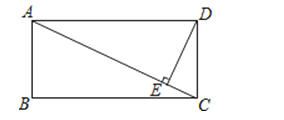
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于函数y=﹣x+3,下列结论正确的是( )
A. 它的图象必经过点(1,1) B. 它的图象经过第一、二、三象限
C. 它的图象与y轴的交点坐标为(0,3) D. y随x的增大而增大
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC在第一象限,OA,OC分别于x轴,y轴重合,面积为6.矩形与双曲线y=
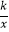 (x>0)交BC于M,交BA于N,连接OB,MN,若2OB=3MN,则k=
(x>0)交BC于M,交BA于N,连接OB,MN,若2OB=3MN,则k= 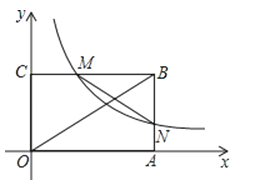
-
科目: 来源: 题型:
查看答案和解析>>【题目】若2x3yn+1与﹣5xm﹣2y2是同类项,则m+n= .
相关试题

