【题目】如图,已知直线y=﹣![]() x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣
x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣![]() x2+2x+5上的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣
x2+2x+5上的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣![]() x+3于点Q,则当PQ=BQ时,a的值是_____.
x+3于点Q,则当PQ=BQ时,a的值是_____.

参考答案:
【答案】-1,4,4+2![]() ,4-2
,4-2![]() .
.
【解析】
试题解析:设点P的坐标为(a,-![]() a2+2a+5),
a2+2a+5),
则点Q为(a,-![]() a+3),点B为(0,3),
a+3),点B为(0,3),
①当点P在点Q上方时,BQ=![]() ,
,
PQ=-![]() a2+2a+5-(-
a2+2a+5-(-![]() a+3)=-
a+3)=-![]() a2+
a2+![]() a+2,
a+2,
∵PQ=BQ,
当a>0时,
∴![]() a=-
a=-![]() a2+
a2+![]() a+2,
a+2,
整理得:a2-3a-4=0,
解得:a=-1(舍去)或a=4,
当a<0时,则-![]() a=-
a=-![]() a2+
a2+![]() a+2,
a+2,
解得:a=4+2![]() (舍去)或a=4-2
(舍去)或a=4-2![]() ;
;
②当点P在点Q下方时,BQ=![]() ,
,
PQ=-![]() a+3-(-
a+3-(-![]() a2+2a+5)=
a2+2a+5)=![]() a2-
a2-![]() a-2,
a-2,
由题意得,PQ=BQ,
当a>0时,
则![]() a=
a=![]() a2-
a2-![]() a-2,
a-2,
整理得:a2-8a-4=0,
解得:a=4+2![]() 或a=4-2
或a=4-2![]() (舍去).
(舍去).
当a<0时,则-![]() a=
a=![]() a2-
a2-![]() a-2,,
a-2,,
解得:a=-1或a=4(舍去),
综上所述,a的值为:-1,4,4+2![]() ,4-2
,4-2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长为
 ,宽为
,宽为  的大长方形被分割为
的大长方形被分割为  小块,除阴影
小块,除阴影  ,
, 外,其余
外,其余  块是形状、大小完全相同的小长方形,其较短一边长为
块是形状、大小完全相同的小长方形,其较短一边长为  .
.
(1)每个小长方形较长的一边长是
 (用含
(用含  的代数式表示).
的代数式表示).(2)分别用含
 ,
, 的代数式表示阴影
的代数式表示阴影  ,
, 的面积,并计算阴影 A 的面积与阴影B的面积的差.
的面积,并计算阴影 A 的面积与阴影B的面积的差.(3)当
 时,阴影
时,阴影  与阴影
与阴影  的面积差会随着
的面积差会随着  的变化而变化吗?请你作出判断,并说明理由.
的变化而变化吗?请你作出判断,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的顶角为36°,则这个三角形就是黄金三角形。如图,在△ABC中,BA=BC,D 在边 CB 上,且 DB=DA=AC。

(1)如图1,写出图中所有的黄金三角形,并证明;
(2)若 M为线段 BC上的点,过 M作直线MH⊥AD于 H,分别交直线 AB,AC与点N,E,如图 2,试写出线段 BN、CE、CD之间的数量关系,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=2,点M为正方形ABCD的边CD上的动点(与点C,D不重合),连接BM,作MF⊥BM,与正方形ABCD的外角∠ADE的平分线交于点F.设CM=x,△DFM的面积为y,则y与x之间的函数关系式为________________.
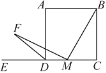
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,使ΔABC≌ΔADC成立的条件是( )

A.AB=AD,∠B=∠DB.AB=AD,∠ACB=ACD
C.BC=DC,∠BAC=∠DACD.AB=AD,∠BAC=∠DAC
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三个盒子中分别装有除颜色外都相同的小球,甲盒中装有两个球,分别为一个红球和一个绿球;乙盒中装有三个球,分别为两个绿球和一个红球;丙盒中装有两个球,分别为一个红球和一个绿球,从三个盒子中各随机取出一个小球
(1)请画树状图,列举所有可能出现的结果
(2)请直接写出事件“取出至少一个红球”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分7分) 已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=
 OB.
OB.(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.

相关试题

