搜索
【题目】如图，已知抛物线y=x2+2x﹣3，把此抛物线沿y轴向上平移，平移后的抛物线和原抛物线与经过点（﹣2，0），（2，0）且平行于y轴的两条直线所围成的阴影部分的面积为s，平移的距离为m，则下列图象中，能表示s与m的函数关系的图象大致是（ ）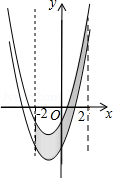
A.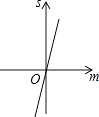
B.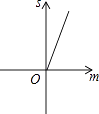
C.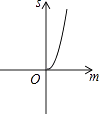
D.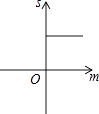
参考答案：
【答案】B
【解析】解：如图，我们把抛物线沿y轴向上平移，平移后的抛物线和原抛物线及直线x=2，x=﹣2所围成的阴影部分的面积S可以看做和矩形BB′C′C等积，于是可以看出S与m是正比例函数关系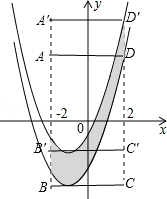
故选：B．
【考点精析】本题主要考查了二次函数图象的平移的相关知识点，需要掌握平移步骤：（1）配方 y=a(x-h)2+k，确定顶点（h,k）（2）对x轴左加右减；对y轴上加下减才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ACB=90°，分别以点A和B为圆心，以相同的长（大于
AB）为半径作弧，两弧相交于点M和N，作直线MN交AB于点D，交BC于点E，连接CD，下列结论错误的是（ ）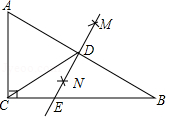 
A.AD=BD
B.BD=CD
C.∠A=∠BED
D.∠ECD=∠EDC -
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在平行四边形OABC中,已知点A、C两点的坐标为A (
,),C (2,0).(1)求点B的坐标.
(2)将平行四边形OABC向左平移
个单位长度,求所得四边形A′B′C′O′四个顶点的坐标.(3)求平行四边形OABC的面积.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，下列条件中，能判断直线L1∥L2的是( )
A. ∠2=∠3 B. ∠l=∠3 C. ∠4+∠5=180
D. ∠2=∠4 -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2E3E4B3…按如图所示的方式放置，其中点B1在y轴上，点C1、E1、E2、C2、E3、E4、C3…在x轴上，已知正方形A1B1C1D1的边长为l，∠B1C1O=60°，B1C1∥B2C2∥B3C3…，则正方形A2017B2017C2017 D2017的边长是（ ）
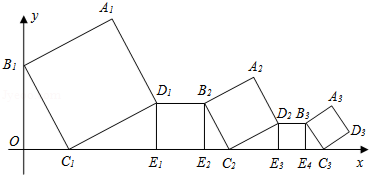
A.（
）2016
B.（ ）2017
C.（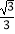
）2016
D.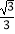（ ）2017 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系上有点A(1．O)，点A第一次跳动至点A1（-1，1）．第四次向右跳动5个单位至点A4(3,2)，…，依此规律跳动下去，点A第100次跳动至点A100的坐标是( )
A. (50，49) B. (51, 49) C. (50, 50) D. (51, 50)
-
科目： 来源： 题型：
查看答案和解析>>【题目】完成证明并写出推理根据
已知，如图，∠1=132
，∠ACB=48，∠2=∠3，FH⊥AB于H，求证：CD⊥AB．
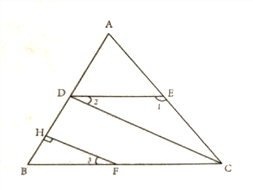
证明:∵∠1=132
, ∠ACB=48∴∠l+∠ACB=180
∴DE∥BC
∴∠2=∠DCB（ ）
又∵∠2=∠3
∴∠3=∠DCB（ ）
∴HF∥DC （ ）
∴∠CDB=∠FHB. （ ）
又∵FH⊥AB,
∴∠FHB=90
∴∠CDB=
∴CD⊥AB. （ ）
相关试题
