搜索
【题目】在平面直角坐标系中，正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2E3E4B3…按如图所示的方式放置，其中点B1在y轴上，点C1、E1、E2、C2、E3、E4、C3…在x轴上，已知正方形A1B1C1D1的边长为l，∠B1C1O=60°，B1C1∥B2C2∥B3C3…，则正方形A2017B2017C2017 D2017的边长是（ ）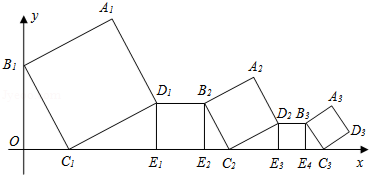 
A.（ 
）2016
B.（ ）2017
C.（ 
）2016
D.（ ）2017
参考答案：
【答案】C
【解析】解：∵正方形A1B1C1D1的边长为1，∠B1C1O=60°，B1C1∥B2C2∥B3C3 ， ∴D1E1=B2E2 ， D2E3=B3E4 ， ∠D1C1E1=∠C2B2E2=∠C3B3E4=30°，
∴D1E1=C1D1sin30°= 
，
则B2C2= 
= 
=（ ）1 ，
同理可得：B3C3= 
=（ ）2 ，
故正方形AnBnCnDn的边长是：（ ）n﹣1 ，
则正方形A2017B2017C2017D2017的边长为：（ ）2016 ，
故选：C．
利用正方形的性质结合锐角三角函数关系得出正方形的边长，进而得出变化规律即可得出答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在平行四边形OABC中,已知点A、C两点的坐标为A (
,),C (2,0).(1)求点B的坐标.
(2)将平行四边形OABC向左平移
个单位长度,求所得四边形A′B′C′O′四个顶点的坐标.(3)求平行四边形OABC的面积.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，下列条件中，能判断直线L1∥L2的是( )
A. ∠2=∠3 B. ∠l=∠3 C. ∠4+∠5=180
D. ∠2=∠4 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y=x2+2x﹣3，把此抛物线沿y轴向上平移，平移后的抛物线和原抛物线与经过点（﹣2，0），（2，0）且平行于y轴的两条直线所围成的阴影部分的面积为s，平移的距离为m，则下列图象中，能表示s与m的函数关系的图象大致是（ ）
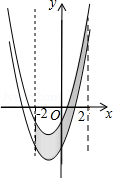
A.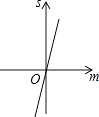
B.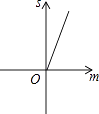
C.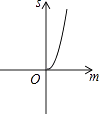
D.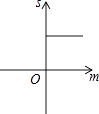
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系上有点A(1．O)，点A第一次跳动至点A1（-1，1）．第四次向右跳动5个单位至点A4(3,2)，…，依此规律跳动下去，点A第100次跳动至点A100的坐标是( )
A. (50，49) B. (51, 49) C. (50, 50) D. (51, 50)
-
科目： 来源： 题型：
查看答案和解析>>【题目】完成证明并写出推理根据
已知，如图，∠1=132
，∠ACB=48，∠2=∠3，FH⊥AB于H，求证：CD⊥AB．
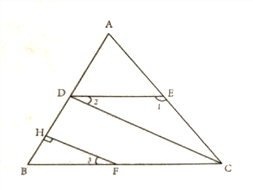
证明:∵∠1=132
, ∠ACB=48∴∠l+∠ACB=180
∴DE∥BC
∴∠2=∠DCB（ ）
又∵∠2=∠3
∴∠3=∠DCB（ ）
∴HF∥DC （ ）
∴∠CDB=∠FHB. （ ）
又∵FH⊥AB,
∴∠FHB=90
∴∠CDB=
∴CD⊥AB. （ ）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的面积为36cm2 ， 点E在BC上，点G在AB的延长线上，四边形EFGB是正方形，以点B为圆心，BC的长为半径画
，连接AF，CF，则图中阴影部分的面积为 ． 
相关试题
