【题目】两条平行直线上各有![]() 个点,用这
个点,用这![]() 个点按如下规则连接线段:
个点按如下规则连接线段:
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出.
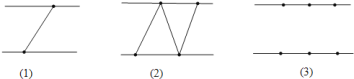
图![]() 展示了当
展示了当![]() 时的情况,此时图中三角形的个数为
时的情况,此时图中三角形的个数为![]() ;图
;图![]() 展示了当
展示了当![]() 时的一种情况,此时图中三角形的个数为
时的一种情况,此时图中三角形的个数为![]() .试回答下列问题:
.试回答下列问题:
![]() 当
当![]() 时,请在图
时,请在图![]() 中画出使三角形个数最少的图形,此时图中三角形的个数是________;
中画出使三角形个数最少的图形,此时图中三角形的个数是________;
![]() 试猜想当有
试猜想当有![]() 对点时,按上述规则画出的图形中,最少有________个三角形;
对点时,按上述规则画出的图形中,最少有________个三角形;
![]() 当
当![]() 时,按上述规则画出的图形中,最少有________个三角形.
时,按上述规则画出的图形中,最少有________个三角形.
参考答案:
【答案】42(n-1)4022
【解析】
(1)根据题意画出图形,根据图形数出三角形个数即可得出答案;
(2)分析可得,当n=1时的情况,此时图中三角形的个数为0,有0=2(11);当n=2时的一种情况,此时图中三角形的个数为2,有2=2(21);…故当有n对点时,最少可以画2(n1)个三角形;
(3)当n=2012时,按上述规则画出的图形中,最少有2×(20121)=4022个三角形.
(1)
如图:
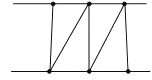
此时图中三角形的个数是:4个;
故答案为:4;
(2)当有n对点时,最少可以画2(n1)个三角形;
故答案为:2(n1);
(3)2×(20121)=4022个,
当n=2012时,最少可以画4022个三角形,
故答案为:4022.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了美化环境,学校准备在如图所示的矩形ABCD空地上进行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ,已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.

(1)分别求y1和y2与x之间的函数关系式(不要求写出自变量的取值范围);
(2)当AN的长为多少米时,种花的面积为440平方米?
(3)若种花每平方米需200元,铺设草坪每平方米需100元,现设计要求种花的面积不大于440平方米,设学校所需费用W(元),求W与x之间的函数关系式,并求出学校所需费用的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+2ax+c的图象与x轴交于A、B两点(点A在点B的左边)AB=4,与y轴交于点C,OC=OA,点D为抛物线的顶点.
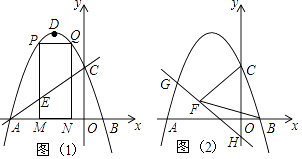
(1)求抛物线的解析式;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM,如图1,点P在点Q左边,当矩形PQNM的周长最大时,求m的值,并求出此时的△AEM的面积;
(3)已知H(0,﹣1),点G在抛物线上,连HG,直线HG⊥CF,垂足为F,若BF=BC,求点G的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=ax+b与y=ax2﹣bx的图象可能是( )
A.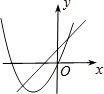
B.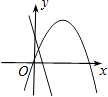
C.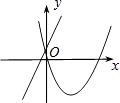
D.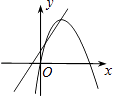
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果多边形的每个内角都比它相邻的外角的4倍多30°,求这个多边形的内角和及对角线的总条数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,能判定△ABC≌△ADC的是( )

A. AC=AC B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D
-
科目: 来源: 题型:
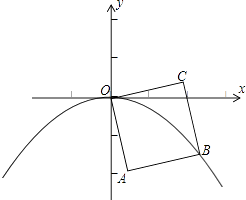
查看答案和解析>>【题目】如图,四边形OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为
相关试题

