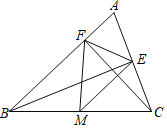
【题目】如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,BC=10.
(1)若∠ABC=50°,∠ACB=60°,求∠EMF的度数;
(2)若EF=4,求△MEF的面积.
参考答案:
【答案】(1)∠EMF=40°;(2)2![]() .
.
【解析】
(1)根据直角三角形的性质得到BM=FM,根据等腰三角形的性质、三角形内角和定理计算;
(2)作MN⊥EF于N,根据直角三角形的性质得到FM=![]() BC=5,根据等腰三角形的性质、三角形面积公式计算.
BC=5,根据等腰三角形的性质、三角形面积公式计算.
解:(1)∵CF⊥AB,M为BC的中点,
∴BM=FM,
∵∠ABC=50°,
∴∠MFB=∠MBF=50°,
∴∠BMF=180°-2×50°=80°,
同理,∠CME═180°-2×60°=60°,
∴∠EMF=180°-∠BMF-∠CME=40°;
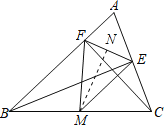
(2)作MN⊥EF于N,
∵CF⊥AB,M为BC的中点,
∴MF是Rt△BFC斜边上的中线,
∴FM=![]() BC=5,
BC=5,
同理可得,ME=5,
∴△EFM是等腰三角形,
∵EF=4,
∴FN=2,
∴MN=![]() =
=![]() ,
,
∴△EFM的面积=![]() EFMN=
EFMN=![]() ×4×
×4×![]() =2
=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两条射线AM∥BN,线段CD的两个端点C、D分别在射线BN、AM上,且∠A=∠BCD=108°.E是线段AD上一点(不与点A、D重合),且BD平分∠EBC.
(1)求∠ABC的度数.
(2)请在图中找出与∠ABC相等的角,并说明理由.
(3)若平行移动CD,且AD>CD,则∠ADB与∠AEB的度数之比是否随着CD位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某乒乓球的质量检验结果如下:
抽取的乒乓球数n
50
100
200
500
1000
1500
2000
优等品的频数m
48
95
188
x
948
1426
1898
优等品的频率
 (精确到0.001)
(精确到0.001)0.960
y
0.940
0.944
z
0.951
0.949
(1)根据表中信息可得:x=______,y=______,z=______;
(2)从这批乒乓球中,任意抽取一只乒乓球是优等品的概率的估计值是多少?(精确到0.01).
-
科目: 来源: 题型:
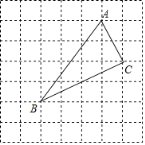
查看答案和解析>>【题目】如图,在7×7网格中,每个小正方形的边长都为1.
(1)建立适当的平面直角坐标系后,若点A(1,3)、C(2,1),则点B的坐标为______;
(2)△ABC的面积为______;
(3)判断△ABC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,把矩形纸片OABC放入直角坐标系xOy中,使OA、OC分别落在x、y轴的正半轴上,连接AC,且AC=4
 ,
, 
(1)求AC所在直线的解析式;
(2)将纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后纸片重叠部分的面积.
(3)求EF所在的直线的函数解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人相约元旦登山,甲、乙两人距地面的高度y(m)与登山时间x(min)之间的函数图像如图所示,根据图像所提供的信息解答下列问题:
(1)t= min.
(2)若乙提速后,乙登山的上升速度是甲登山的上升速度3倍,
①则甲登山的的上升速度是 m/min;
②请求出甲登山过程中,距地面的高度y(m)与登山时间x(min)之间的函数关系式.
③当甲、乙两人距地面高度差为70m时,求x的值(直接写出满足条件的x值).

-
科目: 来源: 题型:
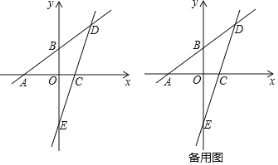
查看答案和解析>>【题目】已知:如图,一次函数y=
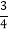 x+3的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
x+3的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.(1)直线CD的函数表达式为______;(直接写出结果)
(2)在x轴上求一点P使△PAD为等腰三角形,直接写出所有满足条件的点P的坐标.
(3)若点Q为线段DE上的一个动点,连接BQ.点Q是否存在某个位置,将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的y轴上?若存在,求点Q的坐标;若不存在,请说明理由.
相关试题

