【题目】如图,两条射线AM∥BN,线段CD的两个端点C、D分别在射线BN、AM上,且∠A=∠BCD=108°.E是线段AD上一点(不与点A、D重合),且BD平分∠EBC.
(1)求∠ABC的度数.
(2)请在图中找出与∠ABC相等的角,并说明理由.
(3)若平行移动CD,且AD>CD,则∠ADB与∠AEB的度数之比是否随着CD位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值.

参考答案:
【答案】(1)∠ABC=72°;(2)与∠ABC相等的角是∠ADC、∠DCN;(3)不发生变化.比值为![]() .
.
【解析】
(1)由平行线的性质可求得∠A+∠ABC=180°,即可求得答案;
(2)利用平行线的性质可求得∠ADC=∠DCN,∠ADC+∠BCD=180°,则可求得答案;
(3)利用平行线的性质,可求得∠AEB=∠EBC,∠ADB=∠DBC,再结合角平分线的定义可求得答案.
(1)∵AM∥BN,∴∠A+∠ABC=180°,∴∠ABC=180°﹣∠A=180°﹣108°=72°.
(2)与∠ABC相等的角是∠ADC、∠DCN.
∵AM∥BN,∴∠ADC=∠DCN,∠ADC+∠BCD=180°,∴∠ADC=180°﹣∠BCD=180°﹣108°=72°,∴∠DCN=72°,∴∠ADC=∠DCN=∠ABC.
(3)不发生变化.
∵AM∥BN,∴∠AEB=∠EBC,∠ADB=∠DBC.
∵BD平分∠EBC,∴∠DBC![]() ∠EBC,∴∠ADB
∠EBC,∴∠ADB![]() ∠AEB,∴∴
∠AEB,∴∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+3交y轴于点A,交x轴正半轴于点C(3,0),交x轴负半轴于点B(﹣1,0),∠ACB=45°.
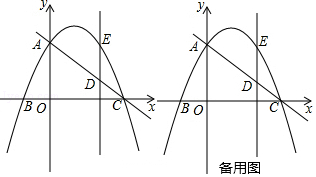
(1)求此抛物线的解析式;
(2)点D为线段AC上一点,且AD=2CD,过点D作DE∥y轴,交抛物线一点E,点P为x轴上方抛物线的一点,设点P的横坐标为t,△PDE的面积为s,求s与t之间的函数关系式,并直接写出t的范围;
(3)在(2)的条件下,过点P作PF∥DE交直线AC于点F,是否存在点P,使以点P、F、E、D为顶点的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一般情况下
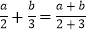 不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得
不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得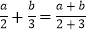 成立的一对数a,b为“相伴数对”,记为(a,b).
成立的一对数a,b为“相伴数对”,记为(a,b).(1)若(1,b)是“相伴数对”,求b的值;
(2)若(m,n)是“相伴数对”,其中m≠0,求
 ;
;(3)若(m,n)是“相伴数对”,求代数式m﹣
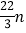 ﹣[4m﹣2(3n﹣1)]的值.
﹣[4m﹣2(3n﹣1)]的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直线l上有A、B、C三个点,已知BC=3AB,点D是AC中点,且BD=6cm,求线段BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年5月份,某市测得一周大气的PM2.5的日均值(单位:微克/立方米)如下:31,35,31,33,30,33,31.对于这组数据下列说法正确的是( )
A.众数是30
B.中位数是31
C.平均数是33
D.方差是32 -
科目: 来源: 题型:
查看答案和解析>>【题目】形如半圆型的量角器直径为4cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的一个端点P、Q,线段PQ交y轴于点A,则点A的坐标为( )

A.(﹣1, )
)
B.(0, )
)
C.( ,0)
,0)
D.(1, )
) -
科目: 来源: 题型:
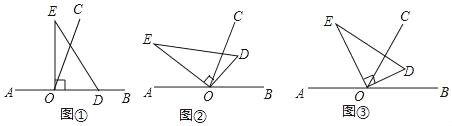
查看答案和解析>>【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OC恰好平分∠BOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O转动,如果OD始终在∠BOC的内部,试猜想∠BOD和∠COE有怎样的数量关系?并说明理由.
相关试题

