【题目】如图所示,把矩形纸片OABC放入直角坐标系xOy中,使OA、OC分别落在x、y轴的正半轴上,连接AC,且AC=4![]() ,
, ![]()
(1)求AC所在直线的解析式;
(2)将纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后纸片重叠部分的面积.
(3)求EF所在的直线的函数解析式.

参考答案:
【答案】(1)y=﹣![]() x+4;(2)重叠部分的面积为10;(3)y=2x﹣6
x+4;(2)重叠部分的面积为10;(3)y=2x﹣6
【解析】试题分析:
(1)设OC=x,则OA=2x,在Rt△AOC中,由勾股定理建立方程,解方程求得x的值,即可得到点A、C的坐标,根据所得A、C两点的坐标用待定系数法求出直线AC的解析式即可;
(2)由折叠的性质可得AE=CE,设AE=CE=y,结合OA=8,可得OE=8-y,在Rt△OCE中由勾股定理建立方程解方程求得y的值即可得到CE的值,再证∠CEF=∠AEF=∠CFE可得CF=CE,这样即可由三角形面积公式求出△CEF的面积了.
(3)由(2)可知OE,CF的长,从而可得点E、F的坐标,由此即可用待定系数法求得直线EF的解析式了.
试题解析:
(1)∵![]() ,
,
∴ 可设OC=x,则OA=2x,
在Rt△AOC中,由勾股定理可得OC2+OA2=AC2,
∴x2+(2x)2=(4![]() )2,解得x=4或x=﹣4(不合题意,舍去),
)2,解得x=4或x=﹣4(不合题意,舍去),
∴OC=4,OA=8,
∴A(8,0),C(0,4),
设直线AC解析式为y=kx+b,
∴![]() ,解得:
,解得: 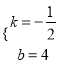 ,
,
∴直线AC解析式为y=![]() x+4;
x+4;
(2)由折叠的性质可知AE=CE,
设AE=CE=y,则OE=8﹣y,
在Rt△OCE中,由勾股定理可得OE2+OC2=CE2,
∴(8﹣y)2+42=y2,解得y=5,
∴AE=CE=5,
∵∠AEF=∠CEF,∠CFE=∠AEF,
∴∠CFE=∠CEF,
∴CE=CF=5,
∴S△CEF=![]() CFOC=
CFOC=![]() ×5×4=10,
×5×4=10,
即重叠部分的面积为10;
(3)由(2)可知OE=3,CF=5,
∴E(3,0),F(5,4),
设直线EF的解析式为y=k′x+b′,
∴![]() ,解得:
,解得: ![]() ,
,
∴直线EF的解析式为y=2x﹣6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某乒乓球的质量检验结果如下:
抽取的乒乓球数n
50
100
200
500
1000
1500
2000
优等品的频数m
48
95
188
x
948
1426
1898
优等品的频率
 (精确到0.001)
(精确到0.001)0.960
y
0.940
0.944
z
0.951
0.949
(1)根据表中信息可得:x=______,y=______,z=______;
(2)从这批乒乓球中,任意抽取一只乒乓球是优等品的概率的估计值是多少?(精确到0.01).
-
科目: 来源: 题型:
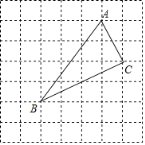
查看答案和解析>>【题目】如图,在7×7网格中,每个小正方形的边长都为1.
(1)建立适当的平面直角坐标系后,若点A(1,3)、C(2,1),则点B的坐标为______;
(2)△ABC的面积为______;
(3)判断△ABC的形状,并说明理由.
-
科目: 来源: 题型:
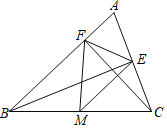
查看答案和解析>>【题目】如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,BC=10.
(1)若∠ABC=50°,∠ACB=60°,求∠EMF的度数;
(2)若EF=4,求△MEF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人相约元旦登山,甲、乙两人距地面的高度y(m)与登山时间x(min)之间的函数图像如图所示,根据图像所提供的信息解答下列问题:
(1)t= min.
(2)若乙提速后,乙登山的上升速度是甲登山的上升速度3倍,
①则甲登山的的上升速度是 m/min;
②请求出甲登山过程中,距地面的高度y(m)与登山时间x(min)之间的函数关系式.
③当甲、乙两人距地面高度差为70m时,求x的值(直接写出满足条件的x值).

-
科目: 来源: 题型:
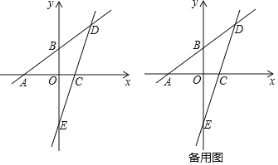
查看答案和解析>>【题目】已知:如图,一次函数y=
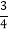 x+3的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
x+3的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.(1)直线CD的函数表达式为______;(直接写出结果)
(2)在x轴上求一点P使△PAD为等腰三角形,直接写出所有满足条件的点P的坐标.
(3)若点Q为线段DE上的一个动点,连接BQ.点Q是否存在某个位置,将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的y轴上?若存在,求点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )

A. AB∥CD,AD∥BC B. OA=OC,OB=OD C. AD=BC,AB∥CD D. AB=CD,AD=BC
相关试题

