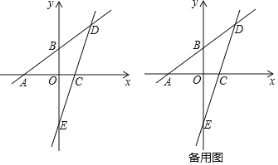
【题目】已知:如图,一次函数y=![]() x+3的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
x+3的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
(1)直线CD的函数表达式为______;(直接写出结果)
(2)在x轴上求一点P使△PAD为等腰三角形,直接写出所有满足条件的点P的坐标.
(3)若点Q为线段DE上的一个动点,连接BQ.点Q是否存在某个位置,将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的y轴上?若存在,求点Q的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=3x-6;(2)点P的坐标为(![]() ,0)或(6,0)或(-14,0)或(12,0);(3)存在,点Q的坐标为(
,0)或(6,0)或(-14,0)或(12,0);(3)存在,点Q的坐标为(![]() ,
,![]() )
)
【解析】
(1)求出D的坐标,即可求解;
(2)分PA=PD、当PA=AD、DP=AD三种情况,分别求解即可;
(3)利用BD=BD′,DQ=D′Q,即可求解.
解:(1)将点D的横坐标为4代入一次函数y=![]() x+3表达式,解得:y=6,即点D的坐标为(4,6),
x+3表达式,解得:y=6,即点D的坐标为(4,6),
将点C、D的坐标代入一次函数表达式y=kx+b得:![]()
解得: ![]()
故答案为:y=3x-6;
(2)①当PA=PD时,
点B是AD的中点,
故:过点B且垂直于AD的直线方程为:y=-![]() x+3,
x+3,
令y=0,则x=![]() ,
,
即点P的坐标为(![]() ,0);
,0);
②当PA=AD时,
AD=![]() =10,
=10,
故点P的坐标为(6,0)或(-14,0);
③当DP=AD时,
同理可得:点P的坐标为(12,0);
故点P的坐标为(![]() ,0)或(6,0)或(-14,0)或(12,0);
,0)或(6,0)或(-14,0)或(12,0);
(3)设翻转后点D落在y轴上的点为D′,设点Q的坐标为(x,3x-6),
则:BD=BD′,DQ=D′Q,
BD′=BD=![]() =5,故点D′的坐标为(0,-2),
=5,故点D′的坐标为(0,-2),
DQ2=D′Q2,即:x2+(3x-6+2)2=(x-4)2+(3x-6-6)2,
解得:x=![]() ,
,
故点Q的坐标为(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
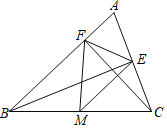
查看答案和解析>>【题目】如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,BC=10.
(1)若∠ABC=50°,∠ACB=60°,求∠EMF的度数;
(2)若EF=4,求△MEF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,把矩形纸片OABC放入直角坐标系xOy中,使OA、OC分别落在x、y轴的正半轴上,连接AC,且AC=4
 ,
, 
(1)求AC所在直线的解析式;
(2)将纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后纸片重叠部分的面积.
(3)求EF所在的直线的函数解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人相约元旦登山,甲、乙两人距地面的高度y(m)与登山时间x(min)之间的函数图像如图所示,根据图像所提供的信息解答下列问题:
(1)t= min.
(2)若乙提速后,乙登山的上升速度是甲登山的上升速度3倍,
①则甲登山的的上升速度是 m/min;
②请求出甲登山过程中,距地面的高度y(m)与登山时间x(min)之间的函数关系式.
③当甲、乙两人距地面高度差为70m时,求x的值(直接写出满足条件的x值).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )

A. AB∥CD,AD∥BC B. OA=OC,OB=OD C. AD=BC,AB∥CD D. AB=CD,AD=BC
-
科目: 来源: 题型:
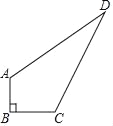
查看答案和解析>>【题目】某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量∠B=90°,AB=3m,BC=4m,CD=12m,AD=13m.若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
-
科目: 来源: 题型:
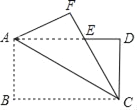
查看答案和解析>>【题目】如图,将长方形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于点E,若AB=4,BC=8,则△ACE的面积为_____.
相关试题

