【题目】如图,抛物线y=ax2+bx+c的顶点为B(1,﹣3),与x轴的一个交点A在(2,0)和(3,0)之间,下列结论中:①bc>0;②2a+b=0;③a﹣b+c>0;④a﹣c=3,正确的有( )个
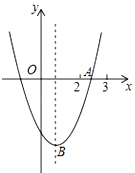
A. 4 B. 3 C. 2 D. 1
参考答案:
【答案】A
【解析】分析: 抛物线开口向上a>0,对称轴在y轴右侧,b<0,抛物线和y轴负半轴相交,c<0,则bc>0,由抛物线与x轴有两个交点得![]() 有抛物线顶点坐标得到抛物线的对称轴为直线x=1,则得到b=2a,即可得到2a+b=0;根据抛物线的对称性得抛物线与x轴的另一个交点B在(0,0)和(1,0)之间,所以当x=1时,y>0,则
有抛物线顶点坐标得到抛物线的对称轴为直线x=1,则得到b=2a,即可得到2a+b=0;根据抛物线的对称性得抛物线与x轴的另一个交点B在(0,0)和(1,0)之间,所以当x=1时,y>0,则![]() ;由抛物线的顶点为D(1,3)得a+b+c=3,由抛物线的对称轴为直线
;由抛物线的顶点为D(1,3)得a+b+c=3,由抛物线的对称轴为直线![]() 得b=2a,所以ac=3.
得b=2a,所以ac=3.
详解: ∵抛物线开口向上,
∴a>0,
∵对称轴在y轴右侧,
∴![]()
∴b<0,
∵抛物线和y轴负半轴相交,
∴c<0,
∴bc>0,故①正确;
∵抛物线的顶点为D(1,3),
∴![]() ,
,
∴b=2a,
∴2a+b=0,故②正确;
∵对称轴为x=1,且与x轴的一个交点A在(2,0)和(3,0)之间,
∴与x轴的另一个交点B在(0,0)和(1,0)之间
∴当x=1时,y>0,
∴y=ab+c>0,故③正确;
∵抛物线的顶点为D(1,3)
∴a+b+c=3,
∵抛物线的对称轴为直线![]() 得b=2a,
得b=2a,
把b=2a代入a+b+c=3,得a2a+c=3,
∴ca=3,
∴ac=3,故④正确;
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我县某公司参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量
 (单位:个)与销售单价
(单位:个)与销售单价 (单位:元/个)之间的关系式为
(单位:元/个)之间的关系式为 .
.(1) 若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润
 (单位:元)与销售单价
(单位:元)与销售单价 (单位:元/个)之间的函数关系式;
(单位:元/个)之间的函数关系式;(2) 在(1)问的条件下,若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示.根据图象所提供的信息有:①甲队挖掘30m时,用了3h;②挖掘6h时甲队比乙队多挖了10m;③乙队的挖掘速度总是小于甲队;④开挖后甲、乙两队所挖河渠长度相等时,x=4.其中一定正确的有( )
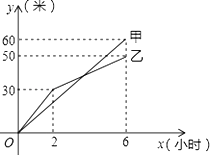
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
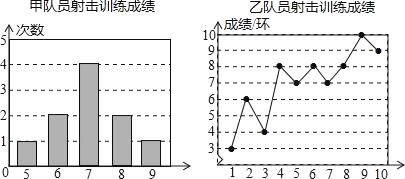
查看答案和解析>>【题目】甲、乙两名队员参加射击训练(各射击10次),成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下表:
平均成绩/环
中位数/环
众数/环
方差/环2
甲
a
7
7
1.2
乙
7
b
8
c
(1)求出表格中a,b,c的值;
(2)分别运用表中的统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是假命题的是( )
A. 在△ABC中,若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
B. 在△ABC中,若a2=(b+c) (b-c),则△ABC是直角三角形
C. 在△ABC中,若∠B=∠C=∠A,则△ABC是直角三角形
D. 在△ABC中,若a:b:c=5:4:3,则△ABC是直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 在平面直角坐标系
在平面直角坐标系 中.
中.
(1)请直接写出点
 、
、 两点的坐标:
两点的坐标: :___________;
:___________; :___________;
:___________;(2)若把
 向上平移3个单位,再向右平移2个单位得
向上平移3个单位,再向右平移2个单位得 ,请在上图中画出
,请在上图中画出 ,并写出点
,并写出点 的坐标___________;
的坐标___________;(3)求
 的面积是多少.
的面积是多少. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读并解决问题:归纳
人们通过长期观察发现,如果早晨天空中有棉絮状的高积云,那么午后常有雷雨降临,于是有了“朝有破絮云,午后雷雨临”的谚语.在数学里,我们也常用这样的方法探求规律,例如:三角形有3个顶点,如果在它的内部再画n个点,并以(n+3)个点为顶点,把三角形剪成若干个小三角形,那么最多可以剪得多少个这样的三角形? .为了解决这个问题,我们可以从n=1、n=2、nr=3 等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.

(1)完成表格信息:_______、_________;
(2)通过观察、比较,可以发现:三角形内的点每增加1个,最多可以剪得的三角形增加_________个.于是,我们可以猜想:当三角形内的点的个数为n时,最多可以剪得____________个三角形.像这样通过对现象的观察、分析,从特殊到-般地探索这类现象的规律、提出猜想的思想方法称为归纳.在日常生活中,人们互相交谈时,常常有人在列举了一些现象后,说“这(即列举的现象)说明....其实这就是运用了归纳的方法.用归纳的方法得出的结论不一定正确,是否正确需要加以证实.
(3)请你借助表格尝试用归纳的方法探索: 1+3+5+7+......+(2n-1)的和是多少?并加以证实.
相关试题

