【题目】阅读并解决问题:归纳
人们通过长期观察发现,如果早晨天空中有棉絮状的高积云,那么午后常有雷雨降临,于是有了“朝有破絮云,午后雷雨临”的谚语.在数学里,我们也常用这样的方法探求规律,例如:三角形有3个顶点,如果在它的内部再画n个点,并以(n+3)个点为顶点,把三角形剪成若干个小三角形,那么最多可以剪得多少个这样的三角形? .为了解决这个问题,我们可以从n=1、n=2、nr=3 等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.

(1)完成表格信息:_______、_________;
(2)通过观察、比较,可以发现:三角形内的点每增加1个,最多可以剪得的三角形增加_________个.于是,我们可以猜想:当三角形内的点的个数为n时,最多可以剪得____________个三角形.像这样通过对现象的观察、分析,从特殊到-般地探索这类现象的规律、提出猜想的思想方法称为归纳.在日常生活中,人们互相交谈时,常常有人在列举了一些现象后,说“这(即列举的现象)说明....其实这就是运用了归纳的方法.用归纳的方法得出的结论不一定正确,是否正确需要加以证实.
(3)请你借助表格尝试用归纳的方法探索: 1+3+5+7+......+(2n-1)的和是多少?并加以证实.
参考答案:
【答案】(1)5,7;(2)2,2n+1;(3)S=n2,见解析
【解析】
(1)由图形规律可得,答案为5,7;
(2)因为5-3=7-5=2,所以三角形内的点每增加1个,最多可以剪得的三角形增加2个;∵三角形内点的个数为1时,最多剪出的小三角形个数3=2×1+1,因为三角形内点的个数为2时,最多剪出的小三角形个数5=2×2+1,三角形内点的个数为3时,7最多剪出的小三角形个数7=2×3+1,所以三角形内点的个数为n时,最多剪出的小三角形个数2n+1;
(3)用倒序相加法证明即可.
(1)把表格补充完整如下:
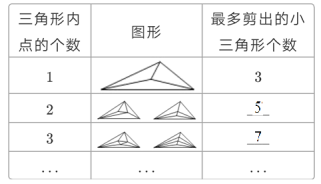
故答案为:5,7;
(2)∵5-3=7-5=2,
∴三角形内的点每增加1个,最多可以剪得的三角形增加2个;
∵三角形内点的个数为1时,最多剪出的小三角形个数3=2×1+1,
三角形内点的个数为2时,最多剪出的小三角形个数5=2×2+1,
三角形内点的个数为3时,7最多剪出的小三角形个数7=2×3+1,
……
∴三角形内点的个数为n时,最多剪出的小三角形个数为2n+1.
故答案为2,(2n+1);
(3)
证明:∵S=1+3+5+7+…+(2n-5)+(2n-3)+(2n-1),
∴S=(2n-1)+(2n-3)+(2n-5)+…+7+5+3+1,
∴S+S=2nn=2n2,
2S=2n2
S=n2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c的顶点为B(1,﹣3),与x轴的一个交点A在(2,0)和(3,0)之间,下列结论中:①bc>0;②2a+b=0;③a﹣b+c>0;④a﹣c=3,正确的有( )个
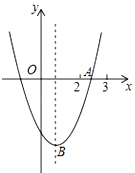
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是假命题的是( )
A. 在△ABC中,若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
B. 在△ABC中,若a2=(b+c) (b-c),则△ABC是直角三角形
C. 在△ABC中,若∠B=∠C=∠A,则△ABC是直角三角形
D. 在△ABC中,若a:b:c=5:4:3,则△ABC是直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 在平面直角坐标系
在平面直角坐标系 中.
中.
(1)请直接写出点
 、
、 两点的坐标:
两点的坐标: :___________;
:___________; :___________;
:___________;(2)若把
 向上平移3个单位,再向右平移2个单位得
向上平移3个单位,再向右平移2个单位得 ,请在上图中画出
,请在上图中画出 ,并写出点
,并写出点 的坐标___________;
的坐标___________;(3)求
 的面积是多少.
的面积是多少. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人约好步行沿同一路线同一方向在某景点集合,已知甲乙二人相距660米,二人同时出发,走了24分钟时,由于乙距离景点近,先到达等候甲,甲共走了30分钟也到达了景点与乙相遇.在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程
 (米)与甲出发的时间
(米)与甲出发的时间 (分钟)之间的关系如图所示,下列说法错误的是( )
(分钟)之间的关系如图所示,下列说法错误的是( )
A.甲的速度是70米/分B.乙的速度是60米/分
C.甲距离景点2100米D.乙距离景点420米
-
科目: 来源: 题型:
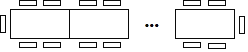
查看答案和解析>>【题目】一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图所示的方式进行拼接.
(1)若把4张这样的餐桌拼接起来,四周可坐 人;
(2)若把n张这样的餐桌拼接起来,四周可坐 人;
(3)若把9张这样的餐桌拼接起来,四周可坐 人;
(4)若用餐的人数有50人,则这样的餐桌需要多少张?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在矩形ABCD中,AD=
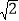 AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,有下列结论:①∠AED=∠CED;②OE=OD;③△BEH≌△HDF;④BC﹣CF=2EH;⑤AB=FH.其中正确的结论有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,有下列结论:①∠AED=∠CED;②OE=OD;③△BEH≌△HDF;④BC﹣CF=2EH;⑤AB=FH.其中正确的结论有( )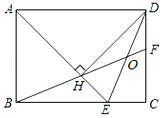
A. 5个 B. 4个 C. 3个 D. 2个
相关试题

