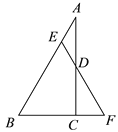
【题目】如图,在 Rt△ABC 中,∠A=30°,∠ACB=90°,点 D 为 AC 中点, 点 E 为 AB 边上一动点,AE=DE,延长 ED 交 BC 的延长线于点 F.
(1)求证:△BEF 是等边三角形;
(2)若 AB=12,求 DE 的长.
参考答案:
【答案】(1)见解析;(2)DE=3.
【解析】
(1)在Rt△ABC 中,∠A=30°,∠ACB=90°,可得∠B=60°,又D 为 AC 中点,AE=DE,可得∠A =∠ADE=30°,可得∠BEF= 60°,△BEF 是等边三角形.
(2) 在 EF 上截取 FG=CF ,连接 CG, 可证得△ADE≌△CDG,AE=CG 设 AE=x,可得BE=12-x,CF=CG=AE=x,BF=6+x,可求x的值,可得DE的长.
(1)A =30°,∠ACB =90°,,
∴∠B=60°.
∵AE=DE,
∴∠A =∠ADE=30°,
∴∠BEF=∠A +∠ADE= 60°.
∴△BEF 是等边三角形.
(2)在 EF 上截取 FG=CF ,连接 CG,
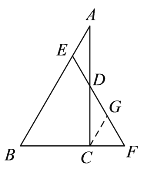
∵∠F=60°,
∴△CFG 为等边三角形.
∴∠FGC =∠F=∠BEF=60°,
∴∠AED =∠CGD,
在△ADE 和△CDG 中,
ADE CDG,AED CGD,AD CD,
∴△ADE≌△CDG(AAS),
∴AE=CG 设 AE=x,则BE=12-x,
∵BC=6,
∴CF=CG=AE=x,
∴BF=6+x,
∴12-x=6+x,,
∴x=3,
∴DE=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系上,△ABC的顶点A和C分别在x轴、y轴的正半轴上,且AB∥y轴,点B(1,3),将△ABC以点B为旋转中心顺时针方向旋转90°得到△DBE,恰好有一反比例函数y=
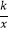 图象恰好过点D,则k的值为( )
图象恰好过点D,则k的值为( ) 
A.6
B.﹣6
C.9
D.﹣9 -
科目: 来源: 题型:
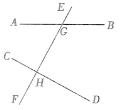
查看答案和解析>>【题目】如图,直线AB,CD被直线EF所截,交点分别为G,H, ∠CHG=∠DHG=
 ∠AGE.
∠AGE.(1)CD与EF有怎样的位置关系?请说明理由.
(2)求∠CHG的同位角、内错角、同旁内角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的四个顶点A、B、C、D正好分别在四条平行线l1、l3、l4、l2上.若从上到下每两条平行线间的距离都是2cm,则正方形ABCD的面积为cm2 .
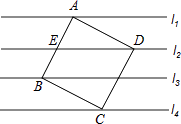
-
科目: 来源: 题型:
查看答案和解析>>【题目】一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150°,求∠ABC的度数.
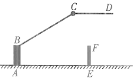
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M是Rt△ABC的斜边AB的中点,连接CM,作线段CM的垂直平分线,分别交边CB和CA的延长线于点D、E,若∠C=90°,AB=20,tanB=
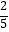 ,则DE= .
,则DE= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,B、C、E 三点在同一条直线上,AB∥DC,BC=DC,∠ACD=∠E.
求证:(1)∠ACB=∠D;
(2)AB=EC.
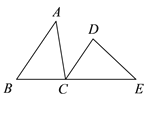
相关试题

