搜索
【题目】如图，在平面直角坐标系上，△ABC的顶点A和C分别在x轴、y轴的正半轴上，且AB∥y轴，点B（1，3），将△ABC以点B为旋转中心顺时针方向旋转90°得到△DBE，恰好有一反比例函数y= 
图象恰好过点D，则k的值为（ ） 
A.6
B.﹣6
C.9
D.﹣9
参考答案：
【答案】B
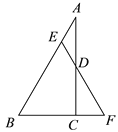
【解析】解：如图， 
∵△ABC以点B为旋转中心顺时针方向旋转90°得到△DBE，点B（1，3），AB∥y轴，
∴BD=BA=3，∠DBA=90°，
∴BD∥x轴，
∴DF=3﹣1=2，
∴D（﹣2，3）．
∵反比例函数y= 
图象恰好过点D，
∴3= 
，解得k=﹣6．
故选B．
先根据旋转的性质得BD=BA=3，∠DBA=90°，则BD∥x轴，易得D（﹣2，3），然后利用待定系数法求反比例函数解析式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知∠AOB是一个直角，作射线OC，再分别作∠AOC和∠BOC的平分线OD，OE．
(1) 如图1，当∠BOC=70°时，求∠DOE的度数．
(2) 如图2，当射线OC在∠AOB内绕点O旋转时，∠DOE的大小是否发生变化?说明理由．
(3) 当射线OC在∠AOB外绕点O旋转且∠AOC为钝角时，画出图形，直接写出相应的∠DOE的度数．(不必写出过程)
-
科目： 来源： 题型：
查看答案和解析>>【题目】体育委员把全班45名同学的体育锻炼时间，并绘制了如图所示的折线统计图，则全班45名同学一周的体育锻炼总时间的众数和中位数分别是（ ）
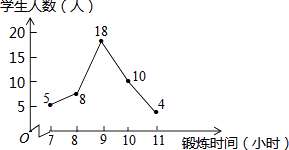
A.9，9
B.9，10
C.18，9
D.18，18 -
科目： 来源： 题型：
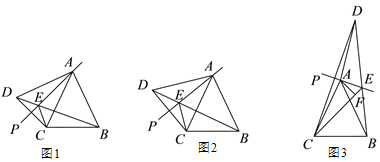
查看答案和解析>>【题目】在△ABC 中，AB=AC，∠CAB=50°.在△ABC 的外侧作直线 AP，作 点 C 关于直线 AP 的对称点 D，连接 BD，CD，AD，其中 BD 交直线 AP 于点 E．
（1）如图 1，与 AD 相等的线段是_____；
（2）如图 2，若∠PAC=20°，求∠BDC 的度数；
（3）如图 3，当 65°<∠PAC<130°时，作 AF⊥CE 于点 F，若 EF=1，BE=5，求 DE 的长．
-
科目： 来源： 题型：
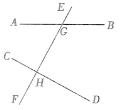
查看答案和解析>>【题目】如图，直线AB，CD被直线EF所截，交点分别为G，H， ∠CHG=∠DHG=
∠AGE.(1)CD与EF有怎样的位置关系？请说明理由.
(2)求∠CHG的同位角、内错角、同旁内角的度数.
-
科目： 来源： 题型：
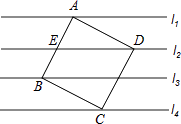
查看答案和解析>>【题目】如图，正方形ABCD的四个顶点A、B、C、D正好分别在四条平行线l1、l3、l4、l2上．若从上到下每两条平行线间的距离都是2cm，则正方形ABCD的面积为cm2 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在 Rt△ABC 中，∠A=30°，∠ACB=90°，点 D 为 AC 中点， 点 E 为 AB 边上一动点，AE=DE，延长 ED 交 BC 的延长线于点 F.
（1）求证：△BEF 是等边三角形；
（2）若 AB=12，求 DE 的长．
相关试题
