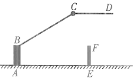
【题目】一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150°,求∠ABC的度数.
参考答案:
【答案】120°.
【解析】
首先过点B作BF∥CD,由CD∥AE,可得CD∥BF∥AE,继而证得∠1+∠BCD=180°,∠2+∠BAE=180°,又由BA垂直于地面AE于A,∠BCD=150°,求得答案.
如图,过点B作 BG∥AE.
∵CD∥AE,
∴BG∥CD,
∴∠GBC+∠BCD =180°.又∠BCD= 150°,
∴∠GBC=180°-∠BCD=180o -150°=30°.
∵BA⊥AE,∴∠BAE = 90°.
∵BG∥AE,
∴∠GBA+∠BAE =180°,
∴∠GBA=180°-∠BAE =90°.
∴∠ABC=∠GBA+∠GBC=90°+30°=120°.
-
科目: 来源: 题型:
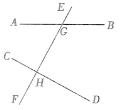
查看答案和解析>>【题目】如图,直线AB,CD被直线EF所截,交点分别为G,H, ∠CHG=∠DHG=
 ∠AGE.
∠AGE.(1)CD与EF有怎样的位置关系?请说明理由.
(2)求∠CHG的同位角、内错角、同旁内角的度数.
-
科目: 来源: 题型:
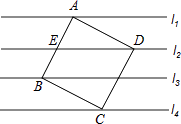
查看答案和解析>>【题目】如图,正方形ABCD的四个顶点A、B、C、D正好分别在四条平行线l1、l3、l4、l2上.若从上到下每两条平行线间的距离都是2cm,则正方形ABCD的面积为cm2 .
-
科目: 来源: 题型:
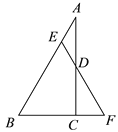
查看答案和解析>>【题目】如图,在 Rt△ABC 中,∠A=30°,∠ACB=90°,点 D 为 AC 中点, 点 E 为 AB 边上一动点,AE=DE,延长 ED 交 BC 的延长线于点 F.
(1)求证:△BEF 是等边三角形;
(2)若 AB=12,求 DE 的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M是Rt△ABC的斜边AB的中点,连接CM,作线段CM的垂直平分线,分别交边CB和CA的延长线于点D、E,若∠C=90°,AB=20,tanB=
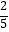 ,则DE= .
,则DE= . 
-
科目: 来源: 题型:
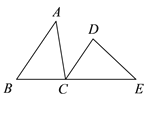
查看答案和解析>>【题目】如图,B、C、E 三点在同一条直线上,AB∥DC,BC=DC,∠ACD=∠E.
求证:(1)∠ACB=∠D;
(2)AB=EC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
相关试题

