Question

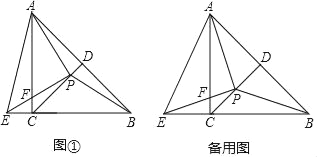
【题目】如图①，在等腰Rt△ABC中，∠ACB＝90°，CD平分∠ACB交AB于点D．点P为线段CD上一点（不与端点C、D重合），PE⊥PA，PE与BC的延长线交于点E，与AC交于点F，连接AE、AP、BP．

（1）求证：AP＝BP；

（2）求∠EAP的度数；

（3）探究线段EC、PD之间的数量关系，并证明．

Answer 1

【答案】（1）见解析；（2）45°；（3）EC＝ PD，理由见解析

【解析】

（1）根据等腰直角三角形的性质可得CD是AB的垂直平分线，根据垂直平分线的性质可得AP＝BP；

（2）由∠ACE＝∠APE＝90°，可得点A，点P，点C，点E四点共圆，可得∠AEP＝∠ACD＝45°，即可求∠EAP的度数；

（3）过点E作EH⊥CD于点H，根据“AAS”可证△APD≌△PEH，可得EH＝PD，根据勾股定理可求EC＝EH，即可得EC＝PD．

证明：（1）∵∠ACB＝90°，AC＝BC，CD平分∠ACB，

∴CD⊥AB，AD＝BD，∠ACD＝∠BCD＝∠CAD＝∠DBC＝45°，

∴CD是AB的垂直平分线

∴AP＝BP，

（2）∵∠ACE＝∠APE＝90°，

∴点A，点P，点C，点E四点共圆，

∴∠AEP＝∠ACD＝45°，且AP⊥EP，

∴∠EAP＝45°

（3）EC＝ PD，理由如下：

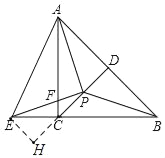
如图，过点E作EH⊥CD于点H，

∵∠EAP＝∠AEP＝45°，

∴AP＝PE，

∵∠APE＝90°＝∠ADP

∴∠APD+∠PAD＝90°，∠APD+∠EPH＝90°，

∴∠PAD＝∠EPH，且AP＝PE，∠EHP＝∠ADP＝90°

∴△APD≌△PEH（AAS）

∴EH＝PD，

∵∠ECH＝∠DCB＝45°，EH⊥CD

∴∠HEC＝∠HCE＝45°

∴EH＝CH

在Rt△ECH中，EC＝＝EH

∴EC＝PD．