搜索
【题目】如图，四边形ABCD中，AD∥BC，∠ABD＝30°，AB＝AD，DC⊥BC于点C，若BD＝2，求CD的长．
参考答案：
【答案】证明：∵ AD="AB"
∴∠ADB＝∠ABD=300
又∵ AD∥BC
∴∠DBC＝∠ABD=300
∵ DC⊥BC ∴△DBC为直角三角形
在Rt△DBC中，∵∠DBC=300
∴CD=
BD=
【解析】
由已知可求得∠ABD＝∠DBC＝30°，已知DC⊥BC，则根据直角三角形中30度所对的边是斜边的一半求解即可．
∵AD∥BC，∴∠ADB＝∠DBC．
又∵AB＝AD，∴∠ADB＝∠ABD，∴∠DBC＝∠ABD＝30°．
∵DC⊥BC于点C，∴∠C＝90°．
在Rt△BDC中，∵∠DBC＝30°，BD＝2，∴CD
，∴CD＝1．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，一次函数y＝k1x+6与x轴、y轴分别交于点A、B两点，与正比例函数y＝k2x交于点D（2，2）
（1）求一次函数和正比例函数的表达式；
（2）若点P（m，m）为直线y＝k2x上的一个动点（点P不与点D重合），点Q在一次函数y＝k1x+6的图象上，PQ∥y轴，当PQ＝
OA时，求m的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
(1)(－2xy)(3x2－2xy－4y2)；
(2)(－
m2n－
mn＋1)·(－6m3n)；(3)(－3x2y)2·(－4xy2－5y3－6x＋1)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】用直尺和圆规作一个角等于已知角，如图，能得出的依据是（ ）
A. SAS B. SSS C. AAS D. ASA
-
科目： 来源： 题型：
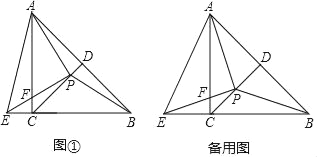
查看答案和解析>>【题目】如图①，在等腰Rt△ABC中，∠ACB＝90°，CD平分∠ACB交AB于点D．点P为线段CD上一点（不与端点C、D重合），PE⊥PA，PE与BC的延长线交于点E，与AC交于点F，连接AE、AP、BP．
（1）求证：AP＝BP；
（2）求∠EAP的度数；
（3）探究线段EC、PD之间的数量关系，并证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，AB＝AC，过点A作GE∥BC，角平分线BD、CF相交于点H，它们的延长线分别交GE于点E、G．试在图中找出3对全等三角形，并对其中一对全等三角形给出证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在等腰Rt△ABC中，∠ACB=90o,AC=CB，F是AB边上的中点,点D、E分别在AC、BC边上运动，且始终保持AD=CE，连接DE、DF、EF．
（1）求证：△ADF≌△CEF；
（2）试证明△DFE是等腰直角三角形．
相关试题
