搜索
【题目】计算：
(1)(－2xy)(3x2－2xy－4y2)；
(2)(－
m2n－
mn＋1)·(－6m3n)；
(3)(－3x2y)2·(－4xy2－5y3－6x＋1)．
参考答案：
【答案】（1）－6x3y＋4x2y2＋8xy3；（2）3m5n2＋2m4n2－6m3n；（3）－36x5y4－45x4y5－54x5y2＋9x4y2.
【解析】
（1）根据多项式乘以多项式的运算法则计算即可求解；（2）根据多项式乘以多项式的运算法则计算即可求解；（3）根据积的乘方的运算法则，先进行乘方运算，再利用多项式乘以多项式的运算法则计算即可求解.
(1)(－2xy)(3x2－2xy－4y2)= －6x3y＋4x2y2＋8xy3；
(2)(－
m2n－
mn＋1)·(－6m3n)= 3m5n2＋2m4n2－6m3n；
(3)(－3x2y)2·(－4xy2－5y3－6x＋1)= 9x4y2·(－4xy2－5y3－6x＋1)= －36x5y4－45x4y5－54x5y2＋9x4y2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．
（1）如图1，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美分割线．
（2）在△ABC中，∠A=48°，CD是△ABC的完美分割线，且AD=CD，求∠ACB的度数．
（3）如图2，△ABC中，AC=2，BC=
，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求完美分割线CD的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
(1)2x3y·(－4xy3z4)；
(2)5a2·(3a3)2；
(3)(－
x2y)3·6x3y4·(3xy2)2. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，一次函数y＝k1x+6与x轴、y轴分别交于点A、B两点，与正比例函数y＝k2x交于点D（2，2）
（1）求一次函数和正比例函数的表达式；
（2）若点P（m，m）为直线y＝k2x上的一个动点（点P不与点D重合），点Q在一次函数y＝k1x+6的图象上，PQ∥y轴，当PQ＝
OA时，求m的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】用直尺和圆规作一个角等于已知角，如图，能得出的依据是（ ）
A. SAS B. SSS C. AAS D. ASA
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD中，AD∥BC，∠ABD＝30°，AB＝AD，DC⊥BC于点C，若BD＝2，求CD的长．
-
科目： 来源： 题型：
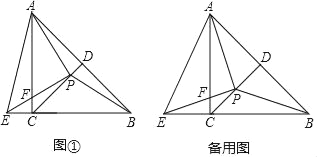
查看答案和解析>>【题目】如图①，在等腰Rt△ABC中，∠ACB＝90°，CD平分∠ACB交AB于点D．点P为线段CD上一点（不与端点C、D重合），PE⊥PA，PE与BC的延长线交于点E，与AC交于点F，连接AE、AP、BP．
（1）求证：AP＝BP；
（2）求∠EAP的度数；
（3）探究线段EC、PD之间的数量关系，并证明．
相关试题
