【题目】在平面直角坐标系![]() 中,对于某点
中,对于某点![]() (
(![]() 不是原点),称以点
不是原点),称以点![]() 为圆心,
为圆心,![]() 长为半径的圆为点
长为半径的圆为点![]() 的半长圆;对于点
的半长圆;对于点![]() ,若将点
,若将点![]() 的半长圆
的半长圆![]() 绕原点旋转,能够使得点
绕原点旋转,能够使得点![]() 位于点
位于点![]() 的半长圆内部或圆上,则称点
的半长圆内部或圆上,则称点![]() 能被点
能被点![]() 半长捕获(或点
半长捕获(或点![]() 能半长捕获点
能半长捕获点![]() ).
).
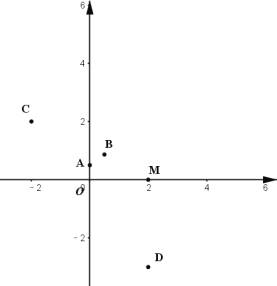
(1)如图,在平面直角坐标系![]() 中,点
中,点![]() ,则点
,则点![]() 的半长圆的面积为__________;下列各点
的半长圆的面积为__________;下列各点![]() 、
、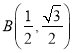 、
、![]() 、
、![]() ,能被点
,能被点![]() 半长捕获的点有__________;
半长捕获的点有__________;
(2)已知点![]() ,
,![]() ,
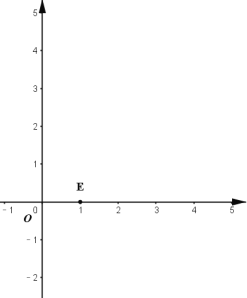
,![]() ,①如图,点
,①如图,点![]() ,当
,当![]() 时,线段
时,线段![]() 上的所有点均可以被点
上的所有点均可以被点![]() 半长捕获,求
半长捕获,求![]() 的取值范围;②若对于平面上的任意点(原点除外)都不能半长捕获线段
的取值范围;②若对于平面上的任意点(原点除外)都不能半长捕获线段![]() 上的所有点,直接写出
上的所有点,直接写出![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)S=π,B、C两点;(2)①-2≤n≤![]() 或
或![]() ≤6n≤2;(2)②
≤6n≤2;(2)②![]() <t<
<t<![]()
【解析】
(1)根据定义,半径为1,直接求面积;根据被捕获的定义,设点到圆心的距离为d,只需r≤d≤3r,即可以捕获;
(2)①利用r≤d≤3r这个性质,分别计算临界点:点E和点F能够被捕获的范围,然后去公共部分即可;
(2)②在上一问的基础上,只需解得的不等式无公共部分,则不能捕获
(1)∵点![]()
∴圆的半径为1,面积为π
根据被捕获的定义,设点到圆心的距离为d,只需r≤d≤3r,即可以捕获
即当1≤d≤3时,点可被捕获
![]() ,则d=
,则d=![]() ,不符合;
,不符合;
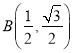 ,d=2,符合;
,d=2,符合;
![]() ,d=2
,d=2![]() ,符合;
,符合;
![]() ,d=
,d=![]() ,不符合
,不符合
(2)①∵点N(0,n)
∴圆的半径为![]() ,所以只需满足
,所以只需满足![]() ≤d≤
≤d≤![]() 时,则可被捕获
时,则可被捕获
点E(1,0),则d=1,要想能够被捕获,则:
![]() ≤1≤
≤1≤![]()
解得:![]() ≤n≤
≤n≤![]() 或
或![]() ≤n≤
≤n≤![]()
点F(1,![]() ),则d=2
),则d=2
同理,![]() ≤2≤
≤2≤![]()
解得:![]() ≤n≤
≤n≤![]() 或
或![]() ≤n≤
≤n≤![]()
合并得:![]() ≤n≤
≤n≤![]() 或
或![]() ≤n≤
≤n≤![]()
(2)②同上,圆的半径为![]() ,所以只需满足
,所以只需满足![]() ≤d≤
≤d≤![]() 时,则可被捕获
时,则可被捕获
点E(t,0),则d=t,要想能够被捕获,则:![]() ≤n≤
≤n≤![]() 或
或![]() ≤n≤
≤n≤![]()
点F(t,![]() ),则d=
),则d=![]() ,要想能够被捕获,则:
,要想能够被捕获,则:![]() ≤n≤
≤n≤![]() 或
或![]() ≤n≤
≤n≤![]()
∵任意值都不能捕获,∴得到的两个不等式无公共部分,即:
![]() 和
和![]() >
>![]()
在结合t>0,解得:0<t<![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
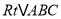 中,
中,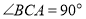 ,
,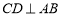 于点
于点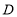 ,
,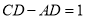 ,为了研究图中线段之间的关系,设
,为了研究图中线段之间的关系,设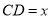 ,
,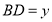 ,
,(1)可通过证明
 ,得到
,得到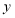 关于
关于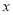 的函数表达式
的函数表达式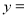 __________,其中自变量
__________,其中自变量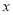 的取值范围是___________;
的取值范围是___________;(2)根据图中给出的(1)中函数图象上的点,画出该函数的图象;
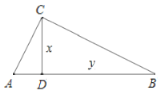

(3)借助函数图象,回答下列问题:①
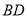 的最小值是__________;②已知当
的最小值是__________;②已知当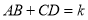 时,
时,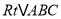 的形状与大小唯一确定,借助函数图象给出
的形状与大小唯一确定,借助函数图象给出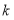 的一个估计值(精确到0.1)或者借助计算给出
的一个估计值(精确到0.1)或者借助计算给出 的精确值.
的精确值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
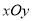 中,抛物线
中,抛物线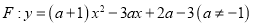
(1)当
 时,求抛物线
时,求抛物线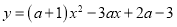 的顶点坐标;
的顶点坐标;(2)已知点
 ,抛物线
,抛物线 与
与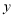 轴交于点
轴交于点 (不与
(不与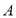 重合),将点
重合),将点 绕点
绕点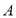 逆时针旋转90°至点
逆时针旋转90°至点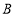 ,
,①直接写出点
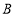 的坐标(用含
的坐标(用含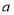 的代数式表示);
的代数式表示);②若抛物线
 与线段
与线段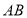 有且仅有一个公共点,求
有且仅有一个公共点,求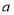 的取值范围.
的取值范围. -
科目: 来源: 题型:
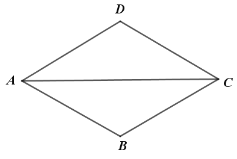
查看答案和解析>>【题目】如图,四边形
 是菱形,且
是菱形,且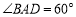 ,点
,点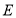 是对角线
是对角线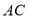 上一点,
上一点,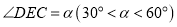 ,绕点
,绕点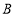 逆时针旋转射线
逆时针旋转射线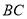 ,旋转角度为
,旋转角度为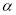 ,并交射线
,并交射线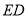 于点
于点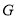 ,连接
,连接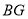 ,
,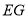 ,
, ,
,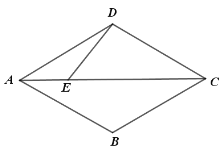
(1)①当
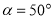 时,补全图形,并证明
时,补全图形,并证明 ;
;
②当
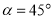 时,直接写出线段
时,直接写出线段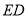 ,
,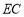 ,
,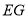 之间的关系;
之间的关系;(2)在平面上找到一点
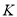 ,使得对于任意的
,使得对于任意的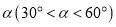 ,总有
,总有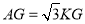 ,直接写出点
,直接写出点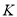 的位置.
的位置.(3)选择下面任意一问回答即可(全卷最多不超过100分)
A.证明(1)②的结论.
B.根据(2)中找到的
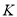 的位置,证明
的位置,证明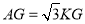
-
科目: 来源: 题型:
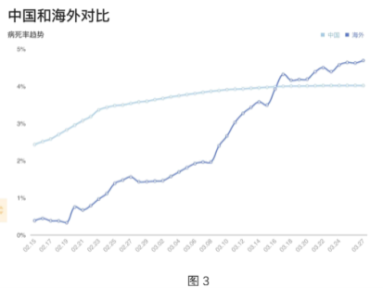
查看答案和解析>>【题目】图1是2020年3月26日全国新冠疫情数据表,图2是3月28日海外各国疫情统计表,图3是中国和海外的病死率趋势对比图,根据这些图表,选出下列说法中错误的一项( )


A.图1显示每天现有确诊数的增加量=累计确诊增加量-治愈人数增加量-死亡人数增加量.
B.图2显示美国累计确诊人数虽然约是德国的两倍,但每百万人口的确诊人数大约只有德国的一半.
C.图2显示意大利当前的治愈率高于西班牙.
D.图3显示大约从3月16日开始海外的病死率开始高于中国的病死率
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在喷水池的中心
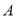 处竖直安装一根水管
处竖直安装一根水管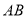 ,水管的顶端安有一个喷水头,使喷出的抛物线形水柱在与池中心
,水管的顶端安有一个喷水头,使喷出的抛物线形水柱在与池中心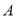 的水平距离为1m处达到最高点
的水平距离为1m处达到最高点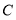 ,高度为3m,水柱落地点
,高度为3m,水柱落地点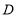 离池中心
离池中心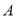 处3m,以水平方向为
处3m,以水平方向为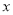 轴,建立平面直角坐标系,若选取点
轴,建立平面直角坐标系,若选取点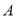 为坐标原点时的抛物线的表达式为
为坐标原点时的抛物线的表达式为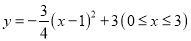 ,则选取点
,则选取点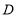 为坐标原点时的抛物线表达式为______,其中自变量的取值范围是______,水管
为坐标原点时的抛物线表达式为______,其中自变量的取值范围是______,水管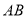 的长为______m.
的长为______m.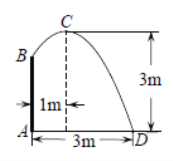
-
科目: 来源: 题型:
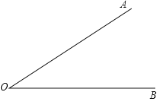
查看答案和解析>>【题目】下面是小华设计的“作一个角等于已知角的2倍”的尺规作图过程.
已知:
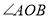 .
.求作:
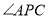 ,使得
,使得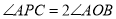 .
.作法:如图,
①在射线
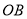 上任取一点
上任取一点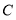 ;
;②作线段
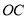 的垂直平分线,交
的垂直平分线,交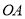 于点
于点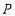 ,交
,交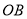 于点
于点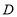 ;
;③连接
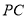 ;
;所以
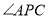 即为所求作的角.
即为所求作的角.根据小华设计的尺规作图过程,
(1)使用直尺和圆规补全图形(保留作图痕迹);
(2)完成下面的证明(说明:括号里填写推理的依据).
证明:∵
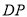 是线段
是线段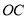 的垂直平分线,
的垂直平分线,∴
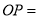 ______(______)
______(______)∴
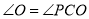 .
.∵
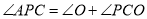 (______)
(______)∴
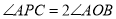 .
.
相关试题

