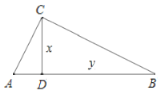
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() ,为了研究图中线段之间的关系,设
,为了研究图中线段之间的关系,设![]() ,
,![]() ,
,
(1)可通过证明![]() ,得到
,得到![]() 关于
关于![]() 的函数表达式
的函数表达式![]() __________,其中自变量
__________,其中自变量![]() 的取值范围是___________;
的取值范围是___________;
(2)根据图中给出的(1)中函数图象上的点,画出该函数的图象;

(3)借助函数图象,回答下列问题:①![]() 的最小值是__________;②已知当
的最小值是__________;②已知当![]() 时,
时,![]() 的形状与大小唯一确定,借助函数图象给出
的形状与大小唯一确定,借助函数图象给出![]() 的一个估计值(精确到0.1)或者借助计算给出
的一个估计值(精确到0.1)或者借助计算给出![]() 的精确值.
的精确值.
参考答案:
【答案】(1)![]() ,x>1;(2)见解析;(3)k≈6.5或k≈-0.5
,x>1;(2)见解析;(3)k≈6.5或k≈-0.5
【解析】
(1)利用相似边之间的关系,可求得x、y之间的关系,结合实际情况,AD>0可得到x的取值范围;
(2)描点绘制函数曲线;
(3)①直接读图可得到;
(3)②△ABC的形状要想唯一,则当k为某一个值时,x、y的值必须为唯一值.x是y的函数,只要x的值唯一,则y的值必定唯一.故只需要将k代入求解,使得x的值为唯一即可
(1)∵∠ACB=90°,CD⊥AB
∴∠A+∠ACD=90°,∠ACD+∠DCB=90°
∴∠A=∠DCB
∵∠ADC=∠CDB=90°
∴△ACD∽△CBD
∵CD-AD=1,CD=x,∴AD=x-1
∴![]() ,代入化简得:y=
,代入化简得:y=![]()
∵AD>0,∴x-1>0,x>1
(2)连接这些点,绘制函数图形如下:
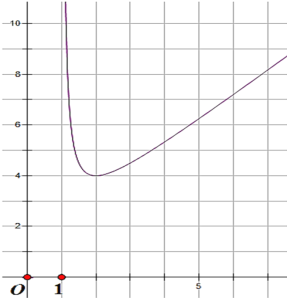
(3)①,由第(2)问的图形可得,y的最小值为4;
(3)②∵AB+CD=k,∴x-1+y+x=k
∵y=![]() ,代入得:2x-1+
,代入得:2x-1+![]() =k,化简得:
=k,化简得:![]()
∵要使△ABC的图形唯一,则需要使得x、y的值唯一
∴上述以x为未知数的一元二次方程的有一个解
∴△=![]() ,化简得:
,化简得:![]()
解得:k=3±![]()
∴k≈6.5或k≈-0.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出口
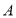 ,
,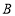 ,
,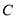 的机动车辆数如图所示,图中
的机动车辆数如图所示,图中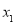 ,
,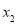 ,
,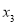 分别表示该时段单位时间通过路段
分别表示该时段单位时间通过路段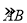 ,
,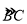 ,
,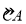 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等).
的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等).(1)若
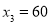 ,
,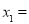 __________.
__________.(2)
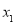 与
与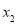 的等量关系为__________.
的等量关系为__________.(3)
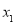 ,
,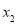 ,
,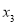 的大小关系为__________.(用>连接).
的大小关系为__________.(用>连接).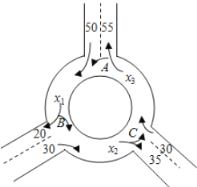
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x
学校
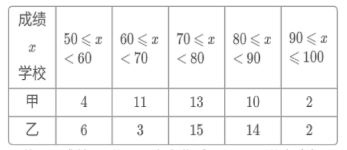

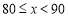

甲
4
11
13
10
2
乙
6
3
15
14
2
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在
 这一组的是:
这一组的是:70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校
平均分
中位数
众数
甲
74.2
n
5
乙
73.5
76
84
根据以上信息,回答下列问题:
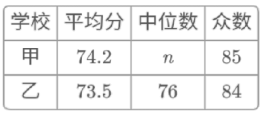
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,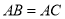 ,点
,点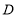 是边
是边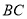 的中点,过点
的中点,过点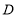 作
作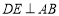 于点
于点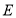 ,
,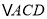 的外接圆与边
的外接圆与边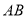 交于点
交于点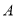 ,
,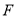 ,
,(1)①补全图形;②判断直线
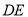 与
与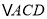 的外接圆的公共点个数,并给出证明.
的外接圆的公共点个数,并给出证明.(2)若
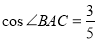 ,
,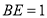 ,求线段
,求线段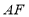 的长度.
的长度.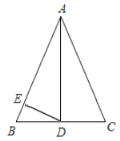
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
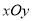 中,抛物线
中,抛物线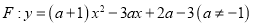
(1)当
 时,求抛物线
时,求抛物线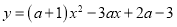 的顶点坐标;
的顶点坐标;(2)已知点
 ,抛物线
,抛物线 与
与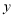 轴交于点
轴交于点 (不与
(不与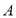 重合),将点
重合),将点 绕点
绕点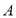 逆时针旋转90°至点
逆时针旋转90°至点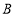 ,
,①直接写出点
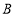 的坐标(用含
的坐标(用含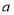 的代数式表示);
的代数式表示);②若抛物线
 与线段
与线段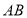 有且仅有一个公共点,求
有且仅有一个公共点,求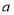 的取值范围.
的取值范围. -
科目: 来源: 题型:
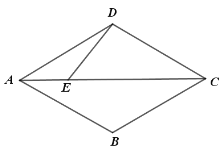
查看答案和解析>>【题目】如图,四边形
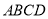 是菱形,且
是菱形,且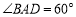 ,点
,点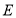 是对角线
是对角线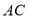 上一点,
上一点,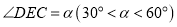 ,绕点
,绕点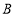 逆时针旋转射线
逆时针旋转射线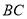 ,旋转角度为
,旋转角度为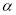 ,并交射线
,并交射线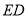 于点
于点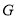 ,连接
,连接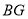 ,
,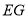 ,
,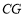 ,
,
(1)①当
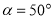 时,补全图形,并证明
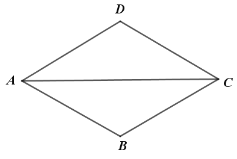
时,补全图形,并证明 ;
;
②当
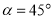 时,直接写出线段
时,直接写出线段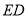 ,
,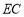 ,
,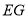 之间的关系;
之间的关系;(2)在平面上找到一点
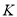 ,使得对于任意的
,使得对于任意的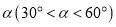 ,总有
,总有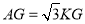 ,直接写出点
,直接写出点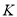 的位置.
的位置.(3)选择下面任意一问回答即可(全卷最多不超过100分)
A.证明(1)②的结论.
B.根据(2)中找到的
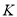 的位置,证明
的位置,证明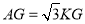
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
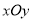 中,对于某点
中,对于某点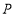 (
(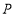 不是原点),称以点
不是原点),称以点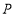 为圆心,
为圆心, 长为半径的圆为点
长为半径的圆为点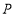 的半长圆;对于点
的半长圆;对于点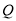 ,若将点
,若将点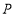 的半长圆
的半长圆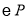 绕原点旋转,能够使得点
绕原点旋转,能够使得点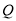 位于点
位于点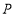 的半长圆内部或圆上,则称点
的半长圆内部或圆上,则称点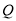 能被点
能被点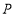 半长捕获(或点
半长捕获(或点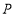 能半长捕获点
能半长捕获点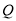 ).
).(1)如图,在平面直角坐标系
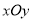 中,点
中,点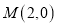 ,则点
,则点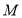 的半长圆的面积为__________;下列各点
的半长圆的面积为__________;下列各点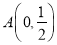 、
、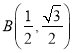 、
、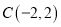 、
、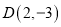 ,能被点
,能被点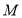 半长捕获的点有__________;
半长捕获的点有__________;(2)已知点
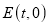 ,
, ,
,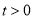 ,①如图,点
,①如图,点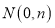 ,当
,当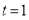 时,线段
时,线段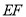 上的所有点均可以被点
上的所有点均可以被点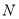 半长捕获,求
半长捕获,求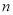 的取值范围;②若对于平面上的任意点(原点除外)都不能半长捕获线段
的取值范围;②若对于平面上的任意点(原点除外)都不能半长捕获线段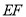 上的所有点,直接写出
上的所有点,直接写出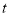 的取值范围.
的取值范围.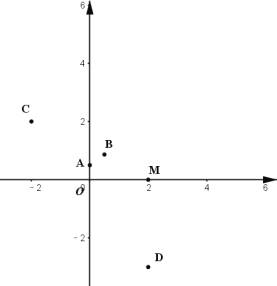
相关试题

