【题目】如图,四边形![]() 是菱形,且
是菱形,且![]() ,点
,点![]() 是对角线
是对角线![]() 上一点,
上一点,![]() ,绕点
,绕点![]() 逆时针旋转射线
逆时针旋转射线![]() ,旋转角度为
,旋转角度为![]() ,并交射线
,并交射线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,
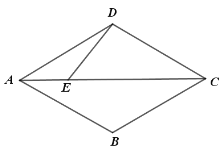
(1)①当![]() 时,补全图形,并证明
时,补全图形,并证明![]() ;
;
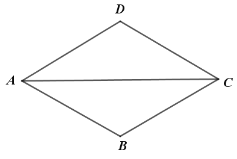
②当![]() 时,直接写出线段
时,直接写出线段![]() ,
,![]() ,
,![]() 之间的关系;
之间的关系;
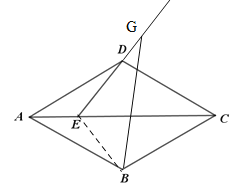
(2)在平面上找到一点![]() ,使得对于任意的
,使得对于任意的![]() ,总有
,总有![]() ,直接写出点
,直接写出点![]() 的位置.
的位置.
(3)选择下面任意一问回答即可(全卷最多不超过100分)
A.证明(1)②的结论. | B.根据(2)中找到的 |
参考答案:
【答案】(1)①见解析;(1)②![]() ;(2)过点G作AG的垂线与AG绕点A顺时针针旋转的交点为k;(3)见解析
;(2)过点G作AG的垂线与AG绕点A顺时针针旋转的交点为k;(3)见解析
【解析】
(1)①连接EB,通过AAS证△CBE≌△EBG;
(1)②将ED转化为EB,EC转化为BG,在Rt△EGB中得到线段直角的关系;
(2)构造含30°的Rt△AGK,即可得到结论;
(3)前2问已证明
(1)①图形如下,连接BE
∵四边形ABCD是菱形,∠BAD=60°
∴∠DCE=∠BCE=30°
∵∠DEC=∠GBC =50°
∴根据菱形的对称性∠BEC=50°,
在△BCE中,
∴∠EBG=180°-∠BCE-∠GBC-∠BEC=50°=∠GEB
∴在△EDC中,∠EDC=100°
∴在四边形ADCB中,∠EBC=100°,∴∠BEC=∠EBG
∵BE=BE
∴△CBE≌△EBG
∴EG=BC
②![]()
(2)如下图,过点G作AG的垂线,交AC于点M,顺时针旋转AG至AK处,使得∠GAD=∠KAC,AK与GM的交点为点K
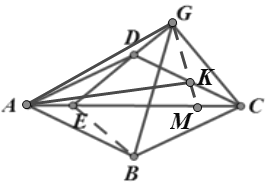
(3)A.
根据菱形的对称性,ED=EB,∠BEC=∠DEC=45°
∴∠GEB=90°,△GEB是直角三角形
∵∠BGE=∠BCE=30°,
则有EG=![]() ,
,
过B点作BH⊥CE于点H,
∵∠CEB=45°,∠ECB=30°,
∴![]()
![]()
∴![]()

B.
∵∠DAC=30°,∠GAD=∠KAC
∴∠GAK=30°
∵AG⊥GM
∴△AGK是直角三角形,且∠GAK=30°
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
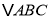 中,
中,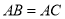 ,点
,点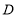 是边
是边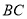 的中点,过点
的中点,过点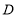 作
作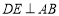 于点
于点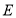 ,
,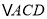 的外接圆与边
的外接圆与边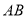 交于点
交于点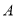 ,
,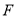 ,
,(1)①补全图形;②判断直线
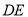 与
与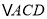 的外接圆的公共点个数,并给出证明.
的外接圆的公共点个数,并给出证明.(2)若
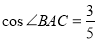 ,
,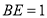 ,求线段
,求线段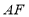 的长度.
的长度.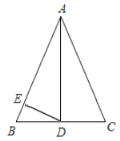
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
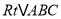 中,
中,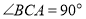 ,
,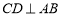 于点
于点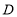 ,
,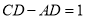 ,为了研究图中线段之间的关系,设
,为了研究图中线段之间的关系,设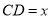 ,
,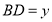 ,
,(1)可通过证明
 ,得到
,得到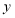 关于
关于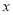 的函数表达式
的函数表达式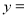 __________,其中自变量
__________,其中自变量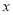 的取值范围是___________;
的取值范围是___________;(2)根据图中给出的(1)中函数图象上的点,画出该函数的图象;
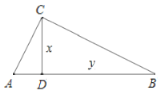

(3)借助函数图象,回答下列问题:①
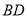 的最小值是__________;②已知当
的最小值是__________;②已知当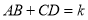 时,
时,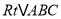 的形状与大小唯一确定,借助函数图象给出
的形状与大小唯一确定,借助函数图象给出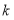 的一个估计值(精确到0.1)或者借助计算给出
的一个估计值(精确到0.1)或者借助计算给出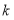 的精确值.
的精确值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
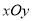 中,抛物线
中,抛物线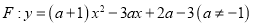
(1)当
 时,求抛物线
时,求抛物线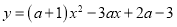 的顶点坐标;
的顶点坐标;(2)已知点
 ,抛物线
,抛物线 与
与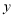 轴交于点
轴交于点 (不与
(不与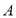 重合),将点
重合),将点 绕点
绕点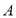 逆时针旋转90°至点
逆时针旋转90°至点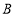 ,
,①直接写出点
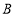 的坐标(用含
的坐标(用含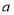 的代数式表示);
的代数式表示);②若抛物线
 与线段
与线段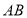 有且仅有一个公共点,求
有且仅有一个公共点,求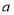 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
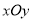 中,对于某点
中,对于某点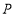 (
(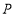 不是原点),称以点
不是原点),称以点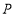 为圆心,
为圆心, 长为半径的圆为点
长为半径的圆为点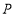 的半长圆;对于点
的半长圆;对于点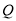 ,若将点
,若将点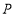 的半长圆
的半长圆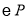 绕原点旋转,能够使得点
绕原点旋转,能够使得点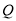 位于点
位于点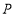 的半长圆内部或圆上,则称点
的半长圆内部或圆上,则称点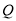 能被点
能被点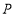 半长捕获(或点
半长捕获(或点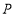 能半长捕获点
能半长捕获点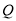 ).
).(1)如图,在平面直角坐标系
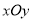 中,点
中,点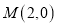 ,则点
,则点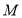 的半长圆的面积为__________;下列各点
的半长圆的面积为__________;下列各点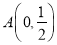 、
、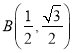 、
、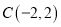 、
、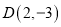 ,能被点
,能被点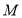 半长捕获的点有__________;
半长捕获的点有__________;(2)已知点
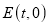 ,
, ,
,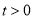 ,①如图,点
,①如图,点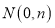 ,当
,当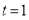 时,线段
时,线段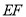 上的所有点均可以被点
上的所有点均可以被点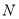 半长捕获,求
半长捕获,求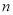 的取值范围;②若对于平面上的任意点(原点除外)都不能半长捕获线段
的取值范围;②若对于平面上的任意点(原点除外)都不能半长捕获线段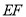 上的所有点,直接写出
上的所有点,直接写出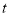 的取值范围.
的取值范围.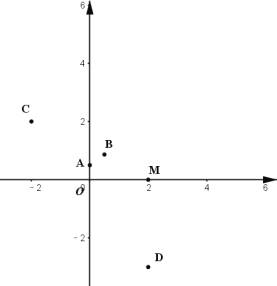
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是2020年3月26日全国新冠疫情数据表,图2是3月28日海外各国疫情统计表,图3是中国和海外的病死率趋势对比图,根据这些图表,选出下列说法中错误的一项( )


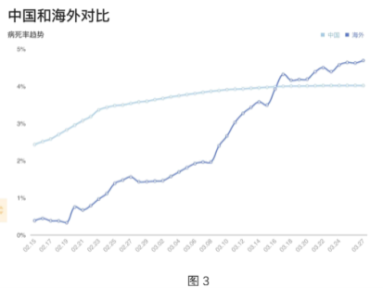
A.图1显示每天现有确诊数的增加量=累计确诊增加量-治愈人数增加量-死亡人数增加量.
B.图2显示美国累计确诊人数虽然约是德国的两倍,但每百万人口的确诊人数大约只有德国的一半.
C.图2显示意大利当前的治愈率高于西班牙.
D.图3显示大约从3月16日开始海外的病死率开始高于中国的病死率
-
科目: 来源: 题型:
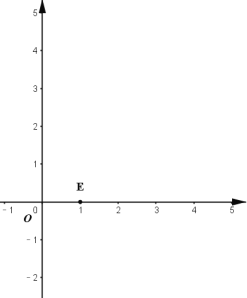
查看答案和解析>>【题目】如图,在喷水池的中心
 处竖直安装一根水管
处竖直安装一根水管 ,水管的顶端安有一个喷水头,使喷出的抛物线形水柱在与池中心
,水管的顶端安有一个喷水头,使喷出的抛物线形水柱在与池中心 的水平距离为1m处达到最高点
的水平距离为1m处达到最高点 ,高度为3m,水柱落地点
,高度为3m,水柱落地点 离池中心
离池中心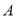 处3m,以水平方向为
处3m,以水平方向为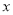 轴,建立平面直角坐标系,若选取点
轴,建立平面直角坐标系,若选取点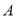 为坐标原点时的抛物线的表达式为
为坐标原点时的抛物线的表达式为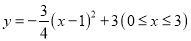 ,则选取点
,则选取点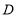 为坐标原点时的抛物线表达式为______,其中自变量的取值范围是______,水管
为坐标原点时的抛物线表达式为______,其中自变量的取值范围是______,水管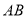 的长为______m.
的长为______m.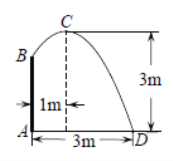
相关试题

