【题目】初中生对待学习的态度一直是教育工作者关注的问题之一.为此市教育局对部分学校的九年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1) 此次抽样调查中,共调查了 名学生;并将图①补充完整;
(2) 求出图中②C级所占的圆心角的度数;
(3) 根据抽样调查结果,请你估计我市近50000名九年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
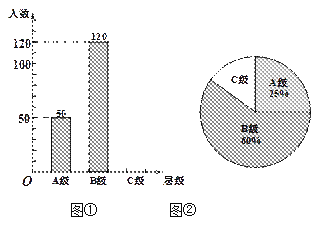
参考答案:
【答案】(1)200;30人(2)54°(3)42500
【解析】试题分析:(1)用A级人数除以A级人数占总人数的比例得到总人数,用总人数减去A级人数减去B级人数得到C级人数;(2)用C级人数除以总人数再乘以360°得到圆心角度数;(3)用50000乘以A和B占的总百分比即可.
试题解析:
(1)50÷25%=200(人),200-50-120=30(人);
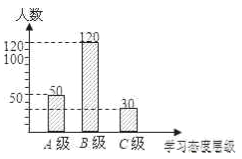
(2)30÷200×360=54°;
(3)50000×(25%+60%)=42500(人).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了1元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2000元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3% 的损耗,第二次购进的水果有4% 的损耗,该水果店希望售完这些水果获利不低于3780元,则该水果每千克售价至少为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系xOy中,抛物线
 与x轴交于点A(﹣1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线
与x轴交于点A(﹣1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线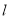 .
.(1)求这条抛物线的关系式,并写出其对称轴和顶点M的坐标;
(2)如果直线y=kx+b经过C、M两点,且与x轴交于点D,点C关于直线
 的对称点为N,试证明四边形CDAN是平行四边形;
的对称点为N,试证明四边形CDAN是平行四边形;(3)点P在直线
 上,且以点P为圆心的圆经过A、B两点,并且与直线CD相切,求点P的坐标.
上,且以点P为圆心的圆经过A、B两点,并且与直线CD相切,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知直线y=﹣
 x+3与x轴、y轴分别交于A、B两点,点C在线段OB上,把△ABC沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )
x+3与x轴、y轴分别交于A、B两点,点C在线段OB上,把△ABC沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )A.(0,﹣
 )B.(0,
)B.(0,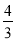 )C.(0,3)D.(0,4)
)C.(0,3)D.(0,4) -
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空:
如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
因为EF∥AD,
所以∠2= .( )
又因为∠1=∠2,
所以∠1=∠3.( )
所以AB∥ .( )
所以∠BAC+ =180°( )
又因为∠BAC=70°,
所以∠AGD= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与坐标轴交于A,B两点,在射线AO上有一点P,当△APB是以AP为腰的等腰三角形时,点P的坐标是________________.
与坐标轴交于A,B两点,在射线AO上有一点P,当△APB是以AP为腰的等腰三角形时,点P的坐标是________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校有A、B两个阅览室,甲、乙、丙三名学生各自随机选择其中的一个阅览室阅读.
(1)下列事件中,是必然事件的为( )
A.甲、乙同学都在A阅览室 B.甲、乙、丙同学中至少两人在A阅览室
C.甲、乙同学在同一阅览室 D.甲、乙、丙同学中至少两人在同一阅览室
(2)用画树状图的方法求甲、乙、丙三名学生在同一阅览室阅读的概率.
相关试题

