【题目】若关于x的方程x2﹣ ![]() +cosα=0有两个相等的实数根,则锐角α为( )
+cosα=0有两个相等的实数根,则锐角α为( )
A.30°
B.45°
C.60°
D.75°
参考答案:
【答案】C
【解析】解:∵关于x的方程x2﹣ ![]() +cosα=0有两个相等的实数根, ∴△=0,
+cosα=0有两个相等的实数根, ∴△=0,
即 ![]() ﹣4×1×cosα=0,
﹣4×1×cosα=0,
∴cosα= ![]() ,
,
∴α=60°.
故选C.
【考点精析】关于本题考查的求根公式和特殊角的三角函数值,需要了解根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在AB上.
(1)试找出∠1,∠2,∠3之间的关系并说出理由;
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1,0),C(0,﹣3).
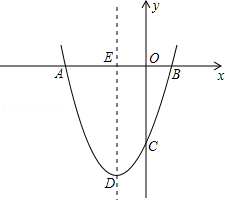
(1)求抛物线的解析式;
(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某轮船由西向东航行,在 A 处测得小岛 P 的方位是北偏东 75°,又继续航行 8 海里后,在 B 处测得小岛 P 的方位是北偏东 60°,则此时△ABP 的面积为______平方海里.
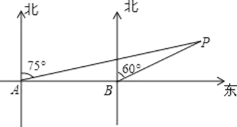
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠B=45°,以点A为圆心的扇形与BC,CD相切,向这样一个靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )
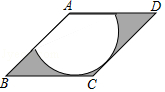
A.1﹣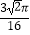
B.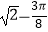
C.1﹣
D.
-
科目: 来源: 题型:
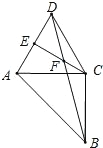
查看答案和解析>>【题目】.如图,以等腰直角△ABC 的直角边 AC 作等边△ACD,CE⊥AD 于 E, BD、CE 交于点 F.
(1)求∠DFE 的度数;
(2)求证:AB=2DF.
相关试题

