搜索
【题目】如图，在菱形ABCD中，∠B=45°，以点A为圆心的扇形与BC，CD相切，向这样一个靶子上随意抛一枚飞镖，则飞镖插在阴影区域的概率为（ ）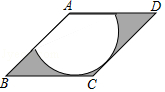 
A.1﹣ 
B.
C.1﹣ 
D.
参考答案：
【答案】A
【解析】解：如图，设切点为E，F，连接AE， ∵以点A为圆心的扇形与BC，CD相切，
∴AE⊥BC，
∵∠B=45°，
∴AE=BE= 
AB，∠BAC=135°，
∴S菱形ABCD=BCAE= AB2 ，
S阴影=S菱形﹣S扇形= AB2﹣ 
= 
πAB2 ，
∴飞镖插在阴影区域的概率=1﹣ 
，
故选A．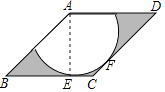
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识，掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径．
-
科目： 来源： 题型：
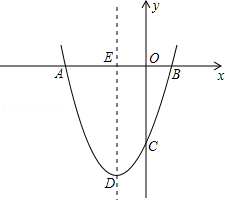
查看答案和解析>>【题目】如图，抛物线y=ax2+bx+c经过点A（﹣3，0），B（1，0），C（0，﹣3）．
（1）求抛物线的解析式；
（2）若点P为第三象限内抛物线上的一点，设△PAC的面积为S，求S的最大值并求出此时点P的坐标；
（3）设抛物线的顶点为D，DE⊥x轴于点E，在y轴上是否存在点M，使得△ADM是直角三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】若关于x的方程x2﹣
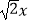+cosα=0有两个相等的实数根，则锐角α为（ ）
A.30°
B.45°
C.60°
D.75° -
科目： 来源： 题型：
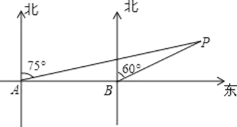
查看答案和解析>>【题目】如图，某轮船由西向东航行，在 A 处测得小岛 P 的方位是北偏东 75°，又继续航行 8 海里后，在 B 处测得小岛 P 的方位是北偏东 60°，则此时△ABP 的面积为______平方海里．
-
科目： 来源： 题型：
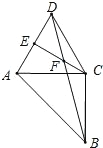
查看答案和解析>>【题目】.如图，以等腰直角△ABC 的直角边 AC 作等边△ACD，CE⊥AD 于 E， BD、CE 交于点 F．
(1)求∠DFE 的度数；
(2)求证：AB=2DF．
-
科目： 来源： 题型：
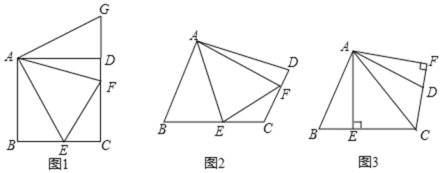
查看答案和解析>>【题目】（1）如图 1，四边形 ABCD 中，∠BAD=∠ADC=∠CBA=90°，AB=AD，点 E、F 分别在四边形 ABCD 的边 BC、CD 上，∠EAF=45°，点 G 在 CD 的延长线上，BE=DG，连接 AG，求证：EF=BE+FD．
(2)如图 2，四边形 ABCD 中，∠BAD≠90°，AB=AD，∠B+∠D=180°，点 E、F 分别在边BC、CD 上，则当∠BAD=2∠EAF 时，仍有 EF=BE+FD 成立吗？说明理由．
(3)如图 3，四边形 ABCD 中，∠BAD≠90°，AB=AD，AC 平分∠BCD，AE⊥BC 于 E，AF⊥CD 交 CD 延长线于 F，若 BC=9，CD=4，则 CE= ．（不需证明）
-
科目： 来源： 题型：
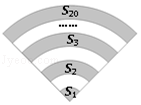
查看答案和解析>>【题目】手机上常见的wifi标志如图所示，它由若干条圆心相同的圆弧组成，其圆心角为90°，最小的扇形半径为1．若每两个相邻圆弧的半径之差为1，由里往外的阴影部分的面积依次记为S1、S2、S3…，则S1+S2+S3+…+S20= ．
相关试题
