【题目】在网格中画对称图形.
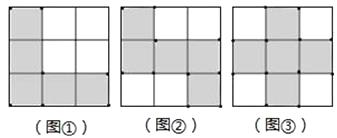
(1)如图是五个小正方形拼成的图形,请你移动其中一个小正方形,重新拼成一个图形,使得所拼成的图形满足下列条件,并分别画在图①、图②、图③中(只需各画一个,内部涂上阴影);
①是轴对称图形,但不是中心对称图形;
②是中心对称图形,但不是轴对称图形;
③既是轴对称图形,又是中心对称图形.
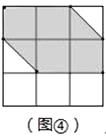
(2)请你在图④的网格内设计一个商标,满足下列要求:
①是顶点在格点的凸多边形(不是平行四边形);
②是中心对称图形,但不是轴对称图形;
③商标内部涂上阴影.
参考答案:
【答案】
(1)解:如图①,是轴对称图形,但不是中心对称图形;
如图②,是中心对称图形,但不是轴对称图形;
如图③,既是轴对称图形,又是中心对称图形.
(2)解:如图④即为所求
【解析】(1)把一个图形沿着一条直线折叠,直线两旁的部分能完全重合的图形就是轴对称图形;把一个图形绕着某一点旋转180 后能与自身重合的图形就是中心对称图形;设计轴对称图形时,先画出图形的一半,然后确定对称轴,再沿着对称轴进行翻折,即可得到完整图形;设计中心对称图形时,先设计出图形的一半,然后确定对称中心,将图形的一半绕对称中心旋转180°,即可得到完整图形,同理,即可设计出既是轴对称图形,又是中心对称图形的图形;
(2)本题是一开放性的命题,根据题目要求以及上述关于轴对称图形和中心对称图形的作图技巧,设计出符合要求的图形即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=
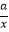 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB. 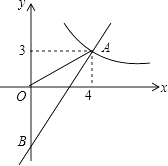
(1)求函数y=kx+b和y=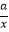 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2-4x-m2=0
(1)求证:该方程有两个不等的实根;
(2)若该方程的两实根x1、x2满足x1+2x2=9,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O的内接四边形ACDB中,AB为直径,AC:BC=1:2,点D为弧AB的中点,BE⊥CD垂足为E.
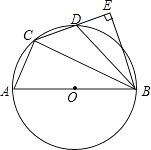
(1)求∠BCE的度数;
(2)求证:D为CE的中点;
(3)连接OE交BC于点F,若AB=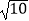 ,求OE的长度.
,求OE的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲同学手中藏有三张分别标有数字
 、
、  、1的卡片,乙同学手中藏有三张分别标有数字1、3、2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
、1的卡片,乙同学手中藏有三张分别标有数字1、3、2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
(1)请你用树形图或列表法列出所有可能的结果;
(2)现制定一个游戏规则:若所选出的a,b能使得ax2+bx+1=0有两个不相等的实数根,则甲获胜;否则乙获胜.请问这样的游戏规则公平吗?请用概率知识解释. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的两条对角线相交于点O,过点A作AG⊥BD分别交BD、BC于点G、E.
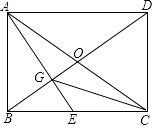
(1)求证:BE2=EGEA;
(2)连接CG,若BE=CE,求证:∠ECG=∠EAC. -
科目: 来源: 题型:
查看答案和解析>>【题目】实数k取何值时,一元二次方程x2-(2k-3)x+2k-4=0:
(1)有两个正根;
(2)有两个异号根,并且正根的绝对值较大;
(3)一根大于3,一根小于3.
相关试题

