【题目】阅读下列材料,然后解决问题:和、差、倍、分等问题中有着广泛的应用,
截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
(1)如图1,在△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是 ;
(2)问题解决:
如图2,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E、F分别是边BC,边CD上的两点,且∠EAF=![]() ∠BAD,求证:BE+DF=EF.
∠BAD,求证:BE+DF=EF.
(3)问题拓展:
如图3,在△ABC中,∠ACB=90°,∠CAB=60°,点D是△ABC外角平分线上一点,DE⊥AC交CA延长线于点E,F是AC上一点,且DF=DB.求证:AC-AE=![]() AF.
AF.

参考答案:
【答案】(1)![]() ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
【解析】
(1)延长AD到点E使DE=AD,连接BE,证明△ADC≌△EDB,根据全等三角形的性质得到BE=AC,根据三角形三边关系计算;
(2)延长CB到G,使BG=DF,证明△ABG≌△ADF,根据全等三角形的性质得到AG=AF,∠GAB=∠FAD,证明△AEG≌△AEF,根据全等三角形的性质证明;
(3)作DH⊥AB于H,在AB上截取BR=AF,分别证明Rt△DEF≌Rt△DHB,△DAF≌△DRB,根据全等三角形的性质证明.
(1)延长AD到点E使DE=AD,连接BE,
在△ADC和△EDB中,
 ,
,
∴△ADC≌△EDB(SAS),
∴BE=AC=8,
AB-BE<AE<AB+BE,即21-8<2AD<12+8,
∴2<AD<10,
故答案为:2<AD<10;
(2)证明:延长CB到G,使BG=DF,

∵∠ABC+∠ADC=180°,∠ABC+∠ABG=180°,
∴∠ADC=∠ABG,
在△ABG和△ADF中,
 ,
,
∴△ABG≌△ADF(SAS),
∴AG=AF,∠GAB=∠FAD,
∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠FAD+∠BAE=∠GAB+∠BAE=![]() ∠BAD,
∠BAD,
∴∠GAE=∠FAE,
在△AEG和△AEF中,
 ,
,
∴△AEG≌△AEF(SAS),
∴EF=GE,
∴EF=BE+BG=BE+DF;
(3)证明:作DH⊥AB于H,在AB上截取BR=AF,

∵∠CAB=60°,∠ACB=90°,
∴∠ABC=30°,
∴AB=2AC,
∵点D是△ABC外角平分线上一点,DE⊥AC,DH⊥AB,
∴DE=DH,AH=AE,
在Rt△DEF和Rt△DHB中,
![]()
∴Rt△DEF≌Rt△DHB(HL)
∴∠DFA=∠DBA,
在△DAF和△DRB中,
 ,
,
∴△DAF≌△DRB(SAS)
∴DA=DR,
∴AH=HR=AE=![]() AR,
AR,
∵AF=BR=AB-AR=2AC-2AE
∴AC-AE=![]() AF.
AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是( )

(A)AB=BE (B)BE⊥DC (C)∠ADB=90° (D)CE⊥DE
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在4×5的网格中,最小正方形的边长为1,A,B,C,D均为格点(最小正方形的顶点).
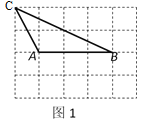
(1)如图1,画出所有以AB为一边且与△ABC全等的格点三角形.
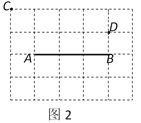
(2)如图2,在线段AB上画出一点P,使CP+PD最小,其最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中, ∠C=90°,边AB的垂直平分线交AB、AC分别于点D,点E,连结BE.

(1)若∠A=40°,求∠CBE的度数.
(2)若AB=10,BC=6,求△BCE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠A=60°,E,F分别是AB,AD的中点,DE,BF相交于点G,连接BD,CG,有下列结论:①∠BGD=120° ;②BG+DG=CG;③△BDF≌△CGB;④
 .其中正确的结论有( )
.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE,则∠DEC的大小为( )

A. 78° B. 45° C. 60° D. 75°
相关试题

