【题目】(1)探究新知:如图1,已知![]() 与
与![]() 的面积相等,试判断
的面积相等,试判断![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
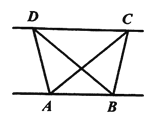
(2)结论应用:
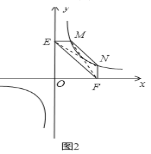
①如图2,点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图像上,过点
的图像上,过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,垂足分别为
轴,垂足分别为![]() ,
,![]() ,连接
,连接![]() .试证明:
.试证明:![]() .
.
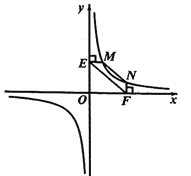
②若①中的其他条件不变,只改变点![]() ,
,![]() 的位置如图3所示,请画出图形,判断
的位置如图3所示,请画出图形,判断![]() 与
与![]() 的位置关系并说明理由.
的位置关系并说明理由.
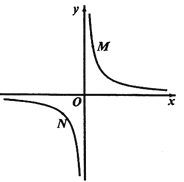
参考答案:
【答案】(1)![]() ,理由见解析;(2)①见解析;②
,理由见解析;(2)①见解析;②![]() ,理由见解析.
,理由见解析.
【解析】
(1)分别过点C,D,作CG⊥AB,DH⊥AB,垂足为G,H,则∠CGA=∠DHB=90°,根据△ABC与△ABD的面积相等,证明AB与CD的位置关系;
(2)连结MF,NE,设点M的坐标为(x1,y1),点N的坐标为(x2,y2),进一步证明S△EFM=S△EFN,结合(1)的结论即可得到MN∥EF;
(3)连接FM、EN、MN,结合(2)的结论证明出MN∥EF,GH∥MN,于是证明出EF∥GH.
(1)如图1,分别过点![]() 、
、![]() 作
作![]() 、
、![]() ,垂足分别为
,垂足分别为![]() 、
、![]() ,
,
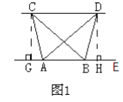
则![]() ,
,
∴![]() ,
,
∵![]() 且
且![]() ,
,
![]() ,
,
∴![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ;
;
(2)①如图2,连接![]() ,
,![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
∵点![]() ,
,![]() 在反比例函数的图像上,
在反比例函数的图像上,
∴![]() ,
,![]() .
.
∵![]() 轴,
轴,![]() 轴,且点
轴,且点![]() ,
,![]() 在第一象限,
在第一象限,
∴![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,
∴![]() ,
,
从而,由(1)中的结论可知:![]() ;
;
②如图
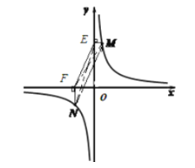
![]() ,
,
理由:连接![]() ,
,![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
由(2)①同理可得:
![]() ,
,![]() ,
,
∴![]() ,
,
从而,由(1)中的结论可知:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美结合.研究数轴我们发现有许多重要的规律:
例如,若数轴上
 点、
点、 点表示的数分别为
点表示的数分别为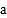 、
、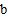 ,则
,则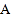 、
、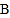 两点之间的距离
两点之间的距离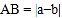 ,线段
,线段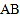 的中点
的中点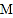 表示的数为
表示的数为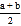 .
.(问题情境)
在数轴上,点
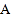 表示的数为-20,点
表示的数为-20,点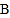 表示的数为10,动点
表示的数为10,动点 从点
从点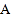 出发沿数轴正方向运动,同时,动点
出发沿数轴正方向运动,同时,动点 也从点
也从点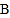 出发沿数轴负方向运动,已知运动到4秒钟时,
出发沿数轴负方向运动,已知运动到4秒钟时, 、
、 两点相遇,且动点
两点相遇,且动点 、
、 运动的速度之比是
运动的速度之比是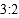 (速度单位:单位长度/秒).
(速度单位:单位长度/秒).

备用图
(综合运用)
(1)点
 的运动速度为______单位长度/秒,点
的运动速度为______单位长度/秒,点 的运动速度为______单位长度/秒;
的运动速度为______单位长度/秒;(2)当
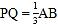 时,求运动时间;
时,求运动时间;(3)若点
 、
、 在相遇后继续以原来的速度在数轴上运动,但运动的方向不限,我们发现:随着动点
在相遇后继续以原来的速度在数轴上运动,但运动的方向不限,我们发现:随着动点 、
、 的运动,线段
的运动,线段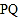 的中点
的中点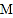 也随着运动.问点
也随着运动.问点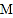 能否与原点重合?若能,求出从
能否与原点重合?若能,求出从 、
、 相遇起经过的运动时间,并直接写出点
相遇起经过的运动时间,并直接写出点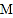 的运动方向和运动速度;若不能,请说明理由.
的运动方向和运动速度;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,点
中,点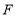 ,
,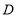 ,
,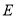 分别是边
分别是边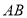 ,
,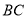 ,
,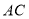 上的点,且
上的点,且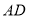 ,
,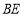 ,
,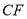 相交于点
相交于点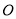 ,若点
,若点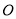 是
是 的重心.则以下结论:①线段
的重心.则以下结论:①线段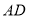 ,
,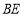 ,
,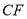 是
是 的三条角平分线;②
的三条角平分线;②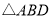 的面积是
的面积是 面积的一半;③图中与
面积的一半;③图中与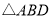 面积相等的三角形有5个;④
面积相等的三角形有5个;④ 的面积是
的面积是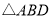 面积的
面积的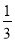 .其中一定正确的结论有( )
.其中一定正确的结论有( )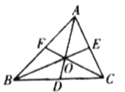
A.①②③B.②④C.③④D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016浙江省衢州市)如图,正方形ABCD的顶点A,B在函数
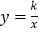 (x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.
(x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.(1)当k=2时,正方形A′B′C′D′的边长等于____.
(2)当变化的正方形ABCD与(1)中的正方形A′B′C′D′有重叠部分时,k的取值范围是______________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,
, ,点
,点 在
在 上,
上, .若点
.若点 是
是 边上异于点
边上异于点 的另一个点,且
的另一个点,且 ,则
,则 的值为______.
的值为______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BD是矩形ABCD的对角线.

(1)用直尺和圆规作线段BD的垂直平分线,分别交AD、BC于E、F(保留作图痕迹,不写作法和证明).
(2)连结BE,DF,问四边形BEDF是什么四边形?请说明理由.
-
科目: 来源: 题型:
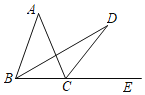
查看答案和解析>>【题目】如图,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,∠D=15°,则∠A=__.
相关试题

