【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美结合.研究数轴我们发现有许多重要的规律:
例如,若数轴上![]() 点、
点、![]() 点表示的数分别为
点表示的数分别为![]() 、
、![]() ,则
,则![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ,线段
,线段![]() 的中点
的中点![]() 表示的数为
表示的数为![]() .
.
(问题情境)
在数轴上,点![]() 表示的数为-20,点
表示的数为-20,点![]() 表示的数为10,动点
表示的数为10,动点![]() 从点
从点![]() 出发沿数轴正方向运动,同时,动点
出发沿数轴正方向运动,同时,动点![]() 也从点
也从点![]() 出发沿数轴负方向运动,已知运动到4秒钟时,
出发沿数轴负方向运动,已知运动到4秒钟时,![]() 、
、![]() 两点相遇,且动点
两点相遇,且动点![]() 、
、![]() 运动的速度之比是
运动的速度之比是![]() (速度单位:单位长度/秒).
(速度单位:单位长度/秒).
![]()
![]()
备用图
(综合运用)
(1)点![]() 的运动速度为______单位长度/秒,点
的运动速度为______单位长度/秒,点![]() 的运动速度为______单位长度/秒;
的运动速度为______单位长度/秒;
(2)当![]() 时,求运动时间;
时,求运动时间;
(3)若点![]() 、
、![]() 在相遇后继续以原来的速度在数轴上运动,但运动的方向不限,我们发现:随着动点
在相遇后继续以原来的速度在数轴上运动,但运动的方向不限,我们发现:随着动点![]() 、
、![]() 的运动,线段
的运动,线段![]() 的中点
的中点![]() 也随着运动.问点
也随着运动.问点![]() 能否与原点重合?若能,求出从
能否与原点重合?若能,求出从![]() 、
、![]() 相遇起经过的运动时间,并直接写出点
相遇起经过的运动时间,并直接写出点![]() 的运动方向和运动速度;若不能,请说明理由.
的运动方向和运动速度;若不能,请说明理由.
参考答案:
【答案】(1)动点P运动的速度为4.5单位长度/秒,动点Q运动的速度为3单位长度/秒;(2)运动时间为![]() 或
或![]() 秒;(3)点M能与原点重合,它沿数轴正方向运动,运动速度为
秒;(3)点M能与原点重合,它沿数轴正方向运动,运动速度为![]() 或沿数轴正方向运动,运动速度为
或沿数轴正方向运动,运动速度为![]() ,理由见解析
,理由见解析
【解析】
(1)设动点P运动的速度分别为3x单位长度/秒,Q运动的速度分别为2x单位长度/秒.根据“运动到4秒钟时,P、Q两点相遇”列方程,求解即可;
(2)设运动时间为t秒.点P表示的数为-20+4.5t,点Q表示的数为10-3t,根据“PQ=![]() AB”,列方程,求解即可;
AB”,列方程,求解即可;
(3)先求出P、Q相遇点表示的数,设从P、Q相遇起经过的运动时间为t秒时,PQ的中点M与原点重合,求出P、Q此时表示的数.然后分四种情况列方程,求解即可.
(1)设动点P运动的速度分别为3x单位长度/秒,Q运动的速度分别为2x单位长度/秒.根据题意得:
4×3x+4×2x=30,(或-20+4×3x=10-4×2x)
解得:x=1.5.
3x=4.5(单位长度/秒),2x=3(单位长度/秒).
答:动点P运动的速度为4.5单位长度/秒,动点Q运动的速度为3单位长度/秒.
(2)设运动时间为t秒.
由题意知:点P表示的数为-20+4.5t,点Q表示的数为10-3t,根据题意得:
|(-20+4.5t)-(10-3t)|=![]() ×|(-20)-10|
×|(-20)-10|
整理得:|7.5t-30|=10
7.5t-30=10或7.5t-30=-10
解得:t=![]() 或t=
或t=![]() .
.
答:运动时间为![]() 或
或![]() 秒.
秒.
(3)P、Q相遇点表示的数为-20+4×4.5=-2(注:当P、Q两点重合时,线段PQ的中点M也与P、Q两点重合)
设从P、Q相遇起经过的运动时间为t秒时,点M与原点重合.
①点P、Q均沿数轴正方向运动,则:
![]()
解得:t=![]() .
.
此时点M能与原点重合,它沿数轴正方向运动,运动速度为2÷![]() (单位长度/秒);
(单位长度/秒);
②点P沿数轴正方向运动,点Q沿数轴负方向运动,则:
![]()
解得:t=![]() .
.
此时点M能与原点重合,它沿数轴正方向运动,运动速度为2÷![]() =
=![]() (单位长度/秒);
(单位长度/秒);
③点P沿数轴负方向运动,点Q沿数轴正方向运动,则:
![]()
解得:t=-![]() (舍去).
(舍去).
此时点M不能与原点重合;
④点P沿数轴负方向运动,点Q沿数轴负方向运动,则:
![]()
解得:t=-![]() (舍去).
(舍去).
此时点M不能与原点重合.
综上所述:点M能与原点重合,它沿数轴正方向运动,运动速度为![]() 或沿数轴正方向运动,运动速度为
或沿数轴正方向运动,运动速度为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1所示,等腰直角三角形ABC中,∠BAC=90O,AB=AC,直线MN经过点A,BD⊥MN于点D,CE⊥MN于点E.
(1)试判断线段DE、BD、CE之间的数量关系,并说明理由;
(2)当直线MN运动到如图2所示位置时,其余条件不变,判断线段DE、BD、CE之间的数量关系。
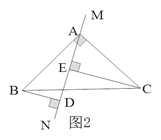
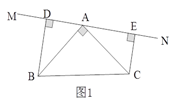
-
科目: 来源: 题型:
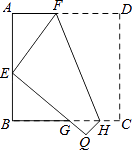
查看答案和解析>>【题目】如图,将正方形纸片ABCD沿FH折叠,使点D与AB的中点E重合,则△FAE与△EBG的面积之比为( )
A.4:9
B.2:3
C.3:4
D.9:16 -
科目: 来源: 题型:
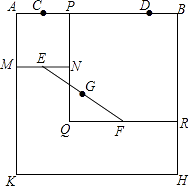
查看答案和解析>>【题目】如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为( )
A.1
B.2
C.3
D.6 -
科目: 来源: 题型:
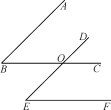
查看答案和解析>>【题目】如图,已知BC,DE相交于点O,给出以下三个判断:①AB∥DE;②BC∥EF;③∠B=∠E,请你以其中两个判断作为题设,另外一个判断作为结论,写出所有的命题,指出这些命题是真命题还是假命题,并选择其中的一个真命题加以证明.
-
科目: 来源: 题型:
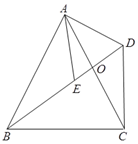
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且AE=AD,∠EAD=∠BAC.
⑴ 求证:∠ABD=∠ACD;
⑵ 若∠ACB=65°,求∠BDC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3种割拼方法,其中能够验证平方差公式的是( )

A. ①② B. ②③ C. ①③ D. ①②③
相关试题

