【题目】如图,已知BD是矩形ABCD的对角线.

(1)用直尺和圆规作线段BD的垂直平分线,分别交AD、BC于E、F(保留作图痕迹,不写作法和证明).
(2)连结BE,DF,问四边形BEDF是什么四边形?请说明理由.
参考答案:
【答案】(1)见解析;(2)四边形BEDF为菱形.见解析
【解析】
试题分析:(1)分别以B、D为圆心,比BD的一半长为半径画弧,交于两点,确定出垂直平分线即可;
(2)连接BE,DF,四边形BEDF为菱形,理由为:由EF垂直平分BD,得到BE=DE,∠DEF=∠BEF,再由AD与BC平行,得到一对内错角相等,等量代换及等角对等边得到BE=BF,再由BF=DF,等量代换得到四条边相等,即可得证.
解:(1)如图所示,EF为所求直线;
(2)四边形BEDF为菱形,理由为:
证明:∵EF垂直平分BD,
∴BE=DE,∠DEF=∠BEF,
∵AD∥BC,
∴∠DEF=∠BFE,
∴∠BEF=∠BFE,
∴BE=BF,
∵BF=DF,
∴BE=ED=DF=BF,
∴四边形BEDF为菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在2,﹣2,3,﹣3这四个数中,最小的数是( )
A. 2 B. -2 C. 3 D. ﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是( )
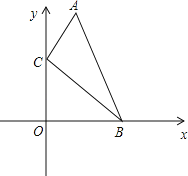
A.(0,0) B.(0,1) C.(0,2) D.(0,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图①、②,解答下面各题:
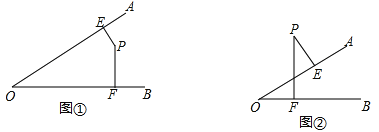
(1)图①中,∠AOB=55°,点P在∠AOB内部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,求∠EPF的度数。
(2)图②中,点P在∠AOB外部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,那么∠P与∠O有什么关系?为什么?
(3)通过上面这两道题,你能说出如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系?
(4)如果一个角的两边分别平行于另一个角的两边,则这两个角是什么关系?(请画图说明结果,不需要过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“绿满鄂南”行动中,某社区计划对面积为1800m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积.
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y与x的函数解析式.
(3)若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,且甲乙两队施工的总天数不超过26天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明所在城市的“阶梯水价”收费办法是:每户用水不超过5吨,每吨水费x元;超过5吨,每吨加收2元,小明家今年5月份用水9吨,共交水费为44元,根据题意列出关于x的方程正确的是( )
A.5x+4(x+2)=44 B.5x+4(x﹣2)=44 C.9(x+2)=44 D.9(x+2)﹣4×2=44
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在九年级第一学期的数学成绩分别为:测验一得88分,测验二得92分,测验三得84分,期中考试得90分,期末考试得87分.如果按照平时、期中、期末的权重分别为10%,30%与60%,那么小明该学期的总评成绩为( )
A. 86 B. 87 C. 88 D. 89
相关试题

