【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() .若点
.若点![]() 是
是![]() 边上异于点
边上异于点![]() 的另一个点,且
的另一个点,且![]() ,则
,则![]() 的值为______.
的值为______.
参考答案:
【答案】24或36或![]()
【解析】
情况1:连接EP交AC于点H,依据先证明![]() 是菱形,再根据菱形的性质可得到∠ECH=∠PCH=60°,然后依据SAS可证明△ECH≌△PCH,则∠EHC=∠PHC=90°,最后依据EP=2EH=2sin60°EC求解即可.
是菱形,再根据菱形的性质可得到∠ECH=∠PCH=60°,然后依据SAS可证明△ECH≌△PCH,则∠EHC=∠PHC=90°,最后依据EP=2EH=2sin60°EC求解即可.
情况2:如图2所示:△ECP为等腰直角三角形,则![]() =
=![]() EC=2
EC=2![]() .此时,
.此时,![]() =24
=24
情况3:如图2:过点P′作P′F⊥BC.通过解直角三角形可以解得FC ,EF,再在Rt△P′EF中,利用勾股定理可以求得![]() .
.
解:情况1:如图所示:连接EP交AC于点H.
∵在![]() 中,
中,![]()
∴![]() 是菱形
是菱形
∵菱形ABCD中,∠B=60°,
∴∠BCD=120°,∠ECH=∠PCH=60°.
在△ECH和△PCH中
 ,
,
∴△ECH≌△PCH.
∴∠EHC=∠PHC=90°,EH=PH.
∴EP=2EH=2sin60°EC=2×![]() ×2
×2![]() =6.
=6.
∴![]() =36
=36
情况2:如图2所示:△ECP为等腰直角三角形,则![]() =
=![]() EC=2
EC=2![]() .
.
∴![]() =24
=24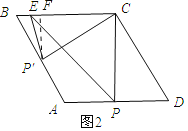
情况3:如图2:过点P′作P′F⊥BC.
∵P′C=2![]() ,BC=4,∠B=60°,
,BC=4,∠B=60°,
∴P′C⊥AB.
∴∠BCP′=30°.
∴FC=![]() ×2
×2![]() =3,P′F=
=3,P′F=![]() ,EF=2
,EF=2![]() -3.
-3.
∴![]() =
=![]()
![]() ,
,
故答案为:24或36或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,点
中,点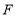 ,
,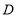 ,
,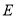 分别是边
分别是边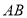 ,
,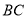 ,
,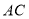 上的点,且
上的点,且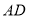 ,
,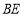 ,
,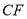 相交于点
相交于点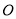 ,若点
,若点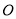 是
是 的重心.则以下结论:①线段
的重心.则以下结论:①线段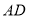 ,
,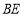 ,
,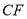 是
是 的三条角平分线;②
的三条角平分线;②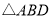 的面积是
的面积是 面积的一半;③图中与
面积的一半;③图中与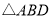 面积相等的三角形有5个;④
面积相等的三角形有5个;④ 的面积是
的面积是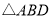 面积的
面积的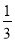 .其中一定正确的结论有( )
.其中一定正确的结论有( )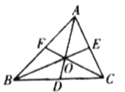
A.①②③B.②④C.③④D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016浙江省衢州市)如图,正方形ABCD的顶点A,B在函数
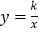 (x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.
(x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.(1)当k=2时,正方形A′B′C′D′的边长等于____.
(2)当变化的正方形ABCD与(1)中的正方形A′B′C′D′有重叠部分时,k的取值范围是______________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)探究新知:如图1,已知
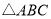 与
与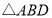 的面积相等,试判断
的面积相等,试判断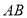 与
与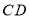 的位置关系,并说明理由.
的位置关系,并说明理由.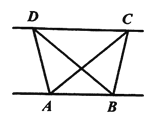
(2)结论应用:
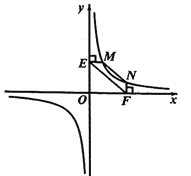
①如图2,点
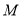 ,
,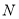 在反比例函数
在反比例函数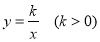 的图像上,过点
的图像上,过点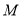 作
作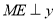 轴,过点
轴,过点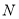 作
作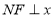 轴,垂足分别为
轴,垂足分别为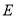 ,
,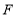 ,连接
,连接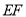 .试证明:
.试证明: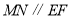 .
.
②若①中的其他条件不变,只改变点
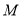 ,
,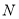 的位置如图3所示,请画出图形,判断
的位置如图3所示,请画出图形,判断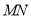 与
与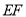 的位置关系并说明理由.
的位置关系并说明理由.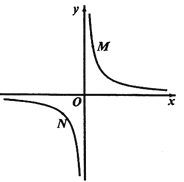
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BD是矩形ABCD的对角线.

(1)用直尺和圆规作线段BD的垂直平分线,分别交AD、BC于E、F(保留作图痕迹,不写作法和证明).
(2)连结BE,DF,问四边形BEDF是什么四边形?请说明理由.
-
科目: 来源: 题型:
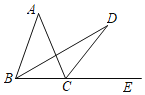
查看答案和解析>>【题目】如图,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,∠D=15°,则∠A=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校组织340名师生进行长途考察活动,带有行李170件,计划租用甲、乙两种型号的汽车共10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.
(1)请你帮助学校设计所有可行的租车方案.
(2)如果甲车的租金为每辆2 000元,乙车的租金为每辆1 800元,问哪种可行方案使租车费用最省?
相关试题

