【题目】如图,已知△ABC和△ECD都是等边三角形,B、C、D在一条直线上。
求证:(1)BE=AD;
(2) △FCH是等边三角形
(3)求∠EMD的度数。

参考答案:
【答案】(1)见解析;(2)见解析;(3)∠EMD=60.
【解析】分析: (1)证明△BCE≌△ACD,再根据全等三角形的性质可得AD=BE; (2)根据全等三角形的性质可得∠BEC=∠ADC,然后根据三角形内角和定理可得∠EMH==∠HCD,进而可得答案.
详解: (1)∵△ABC和△DEC是等边三角形,
∴AC=BC,CE=CD,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
AC=BC,∠BCE=∠ACD,CE=CD,
∴△BCE≌△ACD(SAS),
∴AD=BE.
(2)∵△BCE≌△ACD,
∴∠BCE=∠ADC.
∵∠FCE=∠HCD=60°,
在△FCE和△HCD中,
∠BCE=∠ADC,CE =CD,∠FCE=∠HCD,
∴△BCE≌△ACD (ASA),
∴CF =CH.
在△CFH中,
∵ CF=CH , ∠FCH=60°,
∴△FCH是等边三角形
(3) ∵ △BCE≌△ACD,
∴∠BEC =∠ADC.
在△MHE和△CHD中,
∵∠MEH =∠CDH,
∠MHE =∠CHD(对顶角相等),
∴∠EMH =∠HCD=60°,
∴∠EMD=60.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两工程队承包一项工程,如果甲工程队单独施工,恰好如期完成;如果乙工程队单独施工就要超过6个月才能完成,现在甲、乙两队先共同施工4个月,剩下的由乙队单独施工,则恰好如期完成.
(1)问原来规定修好这条公路需多少长时间?
(2)现要求甲、乙两个工程队都参加这项工程,但由于受到施工场地条件限制,甲、乙两工程队不能同时施工.已知甲工程队每月的施工费用为4万元,乙工程队每月的施工费用为2万元.为了结算方便,要求:甲、乙的施工时间为整数个月,不超过15个月完成.当施工费用最低时,甲、乙各施工了多少个月?
-
科目: 来源: 题型:
查看答案和解析>>【题目】等边△ABC中,点H在边BC上,点K在边AC上,且满足AK=HC,连接AH、BK交于点F.
(1)如图1,求∠AFB的度数;
(2)如图2,连接FC,若∠BFC=90°,点G为边 AC上一点,且满足∠GFC=30°,求证:AG⊥BG
(3)如图3,在(2)条件下,在BF上取D使得DF=AF,连接CD交AH于E,若△DEF面积为1, 则△AHC的面积为

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角梯形ABCD中,AB∥CD,∠ADC=90°,AB=AC,过点B作BE⊥AC于点E.
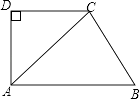
(1)求证:△ADC≌△BEA;
(2)若AD=4,CD=3,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】2013年5月23日起,我市将对行人闯红灯分三档进行处罚,九年级数学研究学习小组在某十字路口随机调查部分市民对该法归的了解情况,统计结果后绘制了如图的三副不完整的统计图,请结合图中相关数据回答下列问题.
得分
A
50<n≤60
B
60<n≤70
C
70<n≤80
D
80<n≤90
E
90<n≤100
(1)本次共调查的人数为;
(2)补全频数分布图;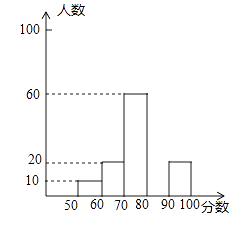
(3)在扇形统计图中,“B”所在的扇形的圆心角的度数为;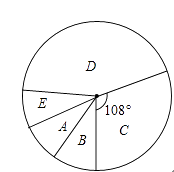
(4)若在这一周里,该路口共有2000人通过,则可估计得分在80以上的人数大约为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为丰富学生的校园生活,准备从友谊体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同、每个篮球的价格相同),若购买3个篮球和2个足球共需420元;购买2个篮球和4个足球共需440元.
(1)购买一个篮球、一个足球各需多少元?
(2)根据该中学的实际情况,需要从该体育用品商店一次性购买足球和篮球共20个.要求购买篮球数不少于足球数的2倍,总费用不超过1840元,那么这所中学有哪几种购买方案?哪种方案所需费用最少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形OABC中,OA=3,AB=6,以OA,OC所在的直线为坐标轴,建立如图1的平面直角坐标系.将矩形OABC绕点O顺时针方向旋转,得到矩形ODEF,当点B在直线DE上时,设直线DE和x轴交于点P,与y轴交于点Q.
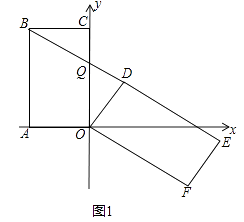
(1)求证:△BCQ≌△ODQ;
(2)求点P的坐标;
(3)若将矩形OABC向右平移(图2),得到矩形ABCG,设矩形ABCG与矩形ODEF重叠部分的面积为S,OG=x,请直接写出x≤3时,S与x之间的函数关系式,并且写出自变量x的取值范围.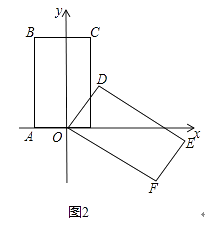
相关试题

