【题目】甲、乙两工程队承包一项工程,如果甲工程队单独施工,恰好如期完成;如果乙工程队单独施工就要超过6个月才能完成,现在甲、乙两队先共同施工4个月,剩下的由乙队单独施工,则恰好如期完成.
(1)问原来规定修好这条公路需多少长时间?
(2)现要求甲、乙两个工程队都参加这项工程,但由于受到施工场地条件限制,甲、乙两工程队不能同时施工.已知甲工程队每月的施工费用为4万元,乙工程队每月的施工费用为2万元.为了结算方便,要求:甲、乙的施工时间为整数个月,不超过15个月完成.当施工费用最低时,甲、乙各施工了多少个月?
参考答案:
【答案】(1) 规定修好路的时间为12个月;(2)工费最低时,甲工作了6个月,乙工作9个月.
【解析】试题分析: ![]() 设规定修好路的时间为x个月,根据工作总量=工作效率
设规定修好路的时间为x个月,根据工作总量=工作效率![]() 工作时间列方程求解即可.
工作时间列方程求解即可.
![]() 甲工作了a月,乙工作了
甲工作了a月,乙工作了![]() 月,列出不等式,求出
月,列出不等式,求出![]() 的取值范围,再分别计算施工费用进行比较即可.
的取值范围,再分别计算施工费用进行比较即可.
试题解析:
(1)设规定修好路的时间为x个月,
![]()
解得:x=12.
检验:当x=12时,x(x+12)≠0.
∴原分子方程的解为x=12,且x=12满足题意.
答:规定修好路的时间为12个月.
(2)甲工作了a月,乙工作了![]() 月(a≤15,b≤15),
月(a≤15,b≤15),
∴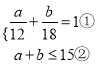 .
.
∴由①可得:b=18-1.5a ③,
代入②中:0<18-1.5a+a≤15,
∴6≤a<12 又a,b均为整数,
∴a=6,b=9,W1=4×6+9×2=42(万元),
a=8,b=6,W2=8×4+6×2=44(万元),
a=10,b=3,W3=10×4+3×2=46(万元),
∵W1<W2<W3,
∴工费最低时,甲工作了6个月,乙工作9个月.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
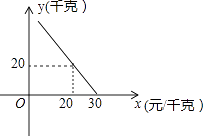
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知单位长度为1的方格中有三角形ABC.
(1)请画出三角形ABC向上平移3格再向右平移2格所得的三角形A′B′C′;
(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),然后写出点B,B′的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】等边△ABC中,点H在边BC上,点K在边AC上,且满足AK=HC,连接AH、BK交于点F.
(1)如图1,求∠AFB的度数;
(2)如图2,连接FC,若∠BFC=90°,点G为边 AC上一点,且满足∠GFC=30°,求证:AG⊥BG
(3)如图3,在(2)条件下,在BF上取D使得DF=AF,连接CD交AH于E,若△DEF面积为1, 则△AHC的面积为

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角梯形ABCD中,AB∥CD,∠ADC=90°,AB=AC,过点B作BE⊥AC于点E.
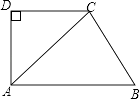
(1)求证:△ADC≌△BEA;
(2)若AD=4,CD=3,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC和△ECD都是等边三角形,B、C、D在一条直线上。
求证:(1)BE=AD;
(2) △FCH是等边三角形
(3)求∠EMD的度数。

相关试题

