【题目】(知识生成)
通常情况下、用两种不同的方法计算同一图形的面积,可以得到一个恒等式.
(1)如图 1,请你写出![]() 之间的等量关系是
之间的等量关系是
(知识应用)
(2)根据(1)中的结论,若![]() ,则
,则![]()
(知识迁移)
类似地,用两种不同的方法计算同一几何体的情况,也可以得到一个恒等式.如图 ![]() 是边长为
是边长为![]() 的正方体,被如图所示的分割成
的正方体,被如图所示的分割成 ![]() 块.
块.
(3)用不同的方法计算这个正方体的体积,就可以得到一个等式,这个等式可以是
(4)已知![]() ,
,![]() ,利用上面的规律求
,利用上面的规律求![]() 的值.
的值.

参考答案:
【答案】(1)![]() .(2)
.(2)![]() .(3)
.(3)![]() .(4)54.
.(4)54.
【解析】
(1)根据两种面积的求法的结果相等,即可得到答案;
(2)根据第(1)问中已知的等式,将数值分别代入,即可求得答案.
(3)根据正方体的体积公式,正方体的边长的立方就是正方体的体积;2个正方体和6个长方体的体积和就是大长方体的体积,则可得到等式;
(4)结合![]() ,
,![]() ,根据(3)中的公式,变形进行求解即可.
,根据(3)中的公式,变形进行求解即可.
(1)![]() .
.
(2)![]() ,
,![]() ,
,![]() 故
故![]() .
.
(3)![]() .
.
(4)由![]() ,
,![]() ,根据第(3)得到的公式可得
,根据第(3)得到的公式可得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(B,F,D在同一条直线上)。一直小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据:
 ≈1.732,
≈1.732,  ≈1.414,结果保留整数)
≈1.414,结果保留整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】仔细阅读下面解方程组的方法,然后解决有关问题:解方程组
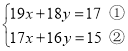 时,如果直接消元,那将会很繁琐,若采用下面的解法,则会简单很多.
时,如果直接消元,那将会很繁琐,若采用下面的解法,则会简单很多.解:①-②,得:2x+2y=2,即x+y=1③
③×16,得:16x+16y=16④
②-④,得:x=-1
将x=-1
代入③得:y=2
∴原方程组的解为:

(1)请你采用上述方法解方程组:

(2)请你采用上述方法解关于x,y的方程组
 ,其中
,其中 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某口罩加工厂有
 两组工人共
两组工人共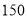 人,
人, 组工人每人每小时可加工口罩
组工人每人每小时可加工口罩 只,
只, 组工人每小时可加工口罩
组工人每小时可加工口罩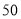 只,
只, 两组工人每小时一共可加工口罩
两组工人每小时一共可加工口罩 只.
只.(1)求
 两组工人各有多少人?
两组工人各有多少人?(2)由于疫情加重,
 两组工人均提高了工作效率,一名
两组工人均提高了工作效率,一名 组工人和一名
组工人和一名 组工人每小时共可生产口罩
组工人每小时共可生产口罩 只,若
只,若 两组工人每小时至少加工
两组工人每小时至少加工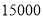 只口罩,那么
只口罩,那么 组工人每人每小时至少加工多少只口罩?
组工人每人每小时至少加工多少只口罩? -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体关系式为
 ,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
(1)求y与x的关系式.
(2)当x取何值时,y的值最大?
(3)如果公司想要在这段时间内获得 元的销售利润,销售单价应定为多少元?
元的销售利润,销售单价应定为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,已知矩形纸片ABCD,AD=2,AB=4,将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB、CD交于点G、F,AE与FG交于点O.
(1)如图1,求证:A、G、E、F四点围成的四边形是菱形;
(2)如图2,点N是线段BC的中点,且ON=OD,求折痕FG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD在平面直角坐标系中,AD=6,若OA、OB的长是关于
 的一元二次方程
的一元二次方程  的两个根,且OA>OB
的两个根,且OA>OB
(1)求cos∠ABC的值。
(2)若E为x轴上的点,且 ,求出点E的坐标,并判断△AOE与△DAO是否相似?请说明理由
,求出点E的坐标,并判断△AOE与△DAO是否相似?请说明理由
相关试题

