搜索
【题目】小敏同学测量一建筑物CD的高度，她站在B处仰望楼顶C，测得仰角为30°，再往建筑物方向走30m，到达点F处测得楼顶C的仰角为45°（B,F,D在同一条直线上）。一直小敏的眼睛与地面距离为1.5m，求这栋建筑物CD的高度（参考数据： 
≈1.732， 
≈1.414，结果保留整数）
参考答案：
【答案】解：延长AE交CD于点G．设CG=xm，
在直角△CGE中，∠CEG=45°，则EG=CG=xm．
在直角△ACG中，AG= 
xm．
∵AG-EG=AE，
∴ 
x-x=30，
解得：x=15（ +1）≈15×2．732≈40．98（m）．
则CD=40．98+1．5=42．48（m）．
答：这栋建筑物CD的高度约为42m
【解析】通过延长AE,把特殊角放到直角三角形中，利用三角函数用CG=x的代数式表示AG、EG，根据线段之差列出方程.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗：我问开店李三公，众客都来到店中，一房七客多七客，一房九客一房空．诗中后两句的意思是：如果每一间客房住7人，那么有7人无房可住；如果每一间客房住9人，那么就空出一间房．
（1）求该店有客房多少间？房客多少人？
（2）假设店主李三公将客房进行改造后，房间数大大增加．每间客房收费20钱，且每间客房最多入住4人，一次性定客房18间以上（含18间），房费按8折优惠．若诗中“众客”再次一起入住，他们如何订房更合算？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，图中的小方格都是边长为1的正方形，△ABC的A，B，C三点坐标为A（2,0）、B（2,2）、C（6，3）。
（1）请在图中画出一个△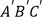
,使△ 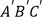与△ABC是以坐标原点为位似中心，相似比为2的位似图形。
（2）求△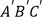 的面积。 -
科目： 来源： 题型：
查看答案和解析>>【题目】在学习了二次根式的相关运算后，我们发现一些含有根号的式子可以表示成另一个式子的平方，如：
3+2
＝2+2+1＝()2+2+1＝(+1)2；5+2
＝2+2
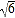+3＝()2+2××
+(
)2＝(+)2(1)请仿照上面式子的变化过程，把下列各式化成另一个式子的平方的形式：
①4+2
；②6+4(2)若a+4
＝(m+n)2，且a，m，n都是正整数，试求a的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】仔细阅读下面解方程组的方法,然后解决有关问题:解方程组
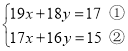时，如果直接消元，那将会很繁琐，若采用下面的解法,则会简单很多.解：①-②，得：2x+2y=2，即x+y=1③
③×16，得：16x+16y=16④
②-④，得：x=-1
将x=-1
代入③得：y=2
∴原方程组的解为：
（1）请你采用上述方法解方程组：
（2）请你采用上述方法解关于x，y的方程组
，其中
． -
科目： 来源： 题型：
查看答案和解析>>【题目】某口罩加工厂有
两组工人共
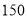人，
组工人每人每小时可加工口罩
只，
组工人每小时可加工口罩
只,两组工人每小时一共可加工口罩
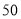只.（1）求
两组工人各有多少人？（2）由于疫情加重，
两组工人均提高了工作效率，一名组工人和一名组工人每小时共可生产口罩
只，若两组工人每小时至少加工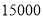
只口罩，那么组工人每人每小时至少加工多少只口罩？ -
科目： 来源： 题型：
查看答案和解析>>【题目】（知识生成）
通常情况下、用两种不同的方法计算同一图形的面积，可以得到一个恒等式.
（1）如图 1，请你写出
之间的等量关系是 （知识应用）
（2）根据（1）中的结论，若
，则
（知识迁移）
类似地，用两种不同的方法计算同一几何体的情况，也可以得到一个恒等式.如图
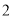是边长为
的正方体，被如图所示的分割成 
块．（3）用不同的方法计算这个正方体的体积，就可以得到一个等式，这个等式可以是
（4）已知
，
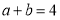，利用上面的规律求
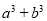的值．
相关试题
