【题目】如图,平行四边形ABCD在平面直角坐标系中,AD=6,若OA、OB的长是关于 ![]() 的一元二次方程
的一元二次方程 ![]() 的两个根,且OA>OB
的两个根,且OA>OB
(1)求cos∠ABC的值。
(2)若E为x轴上的点,且 ![]() ,求出点E的坐标,并判断△AOE与△DAO是否相似?请说明理由
,求出点E的坐标,并判断△AOE与△DAO是否相似?请说明理由
参考答案:
【答案】
(1)解:解一元二次方程 ![]() 得
得 ![]() ,
, ![]() ∵OA>OB ∴OA=4,OB=3,
∵OA>OB ∴OA=4,OB=3,
在 ![]() ,
,
∴ ![]() ,
,
∴cos∠ABC= ![]()
(2)解:设E(x,0),由题意得 ![]() 解得
解得 ![]() ∴E(
∴E( ![]() ,0)或(
,0)或( ![]() ,0), ∵四边形ABCD是平行四边形,
,0), ∵四边形ABCD是平行四边形,
∴点D的坐标是(6,4) 设经过D、E两点的直线的解析式为 ![]() 若图象过点(
若图象过点( ![]() ,0),(6,4) 则
,0),(6,4) 则 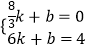 ,解得
,解得 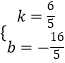 此时函数解析式为
此时函数解析式为 ![]()
若图象过点( ![]() ,0),(6,4) 则
,0),(6,4) 则  ,解得
,解得 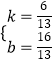 此时函数解析式为
此时函数解析式为 ![]()
在△AOE与△DAO中, ![]() ,
, ![]()
∴ ![]()
又∵∠AOE=∠OAD=90°
∴△AOE∽△DAO。
【解析】(1)可先解一元二次方程求出OA,OB的长度,再利用勾股定理求出AB的长度,利用余弦定义计算得出结果;
(2)先根据三角形的面积求出OE,再转化为坐标,有两种情况,,并根据平行四边形的对边相等的性质求出点D的坐标,然后利用待定系数法求解直线的解析式;分别求出两三角形夹直角的两对应边的比,如果相等,则两三角形相似,否则不相似;
-
科目: 来源: 题型:
查看答案和解析>>【题目】(知识生成)
通常情况下、用两种不同的方法计算同一图形的面积,可以得到一个恒等式.
(1)如图 1,请你写出
 之间的等量关系是
之间的等量关系是 (知识应用)
(2)根据(1)中的结论,若
 ,则
,则
(知识迁移)
类似地,用两种不同的方法计算同一几何体的情况,也可以得到一个恒等式.如图
 是边长为
是边长为 的正方体,被如图所示的分割成
的正方体,被如图所示的分割成  块.
块.(3)用不同的方法计算这个正方体的体积,就可以得到一个等式,这个等式可以是
(4)已知
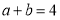 ,
, ,利用上面的规律求
,利用上面的规律求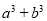 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体关系式为
 ,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
(1)求y与x的关系式.
(2)当x取何值时,y的值最大?
(3)如果公司想要在这段时间内获得 元的销售利润,销售单价应定为多少元?
元的销售利润,销售单价应定为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,已知矩形纸片ABCD,AD=2,AB=4,将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB、CD交于点G、F,AE与FG交于点O.
(1)如图1,求证:A、G、E、F四点围成的四边形是菱形;
(2)如图2,点N是线段BC的中点,且ON=OD,求折痕FG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
 (2)
(2)
(3)
 (4)
(4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC与BD交于点O,AC=6,BD=8.动点E从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止.点F是点E关于BD的对称点,EF交BD于点P,若BP=x,△OEF的面积为y,则y与x之间的函数图象大致为( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AD于点E,交BC于点F,连接BE,DF,且BE平分∠ABD.
①求证:四边形BFDE是菱形;
②直接写出∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.

相关试题

