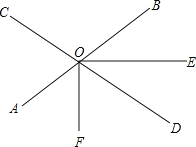
【题目】如图,直线AB、CD相交于O点,∠AOC=70,OF平分∠AOD,射线OE在∠BOD的内部(如图),∠BOE=n°.
(1)当n=30时,求∠DOE的度数;
(2)当n=35时,射线OE与OF之间有什么位置关系?
(3)若射线OD平分∠EOF,求n的值.
参考答案:
【答案】(1)40°;(2)射线OE有OF之间垂直.(3)15
【解析】
(1)根据对顶角相等得到∠DOB=∠AOC=70°,利用∠DOE=∠DOB-∠BOE计算出即可;
(2)根据邻补角的定义得到AOD=180°-∠AOC=180°-70°=110°,再利用角平分线的定义得到![]() 易得∠FOE=∠DOF+∠DOE=55°+35°=90°,根据垂直的定义即可得到射线OE与OF垂直.
易得∠FOE=∠DOF+∠DOE=55°+35°=90°,根据垂直的定义即可得到射线OE与OF垂直.
(3)
(1)∵![]()
∴![]()
(2)射线OE与OF垂直.理由如下:
∵![]()
∴![]()
∵![]()
而OF平分∠AOD,
∴![]()
∴![]()
∴射线OE与OF垂直.
(3) ∵![]()
∴![]()
∵![]()
而OF平分∠AOD,
∴![]()
射线OD平分∠EOF,
![]()
∴![]()
解得:![]()
-
科目: 来源: 题型:
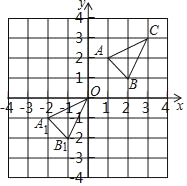
查看答案和解析>>【题目】如图,已知△ABC经过平移后得到△A1B1C1,点A与A1,点B与B1,点C与C1分别是对应点,观察各对应点坐标之间的关系,解答下列问题:
(1)分别写出点A与A1,点B与B1,点C与C1的坐标;
(2)若点P(x,y)通过上述的平移规律平移得到的对应点为Q(3,5),求p点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正△ABC的边长为6,那么能够完全覆盖这个正△ABC的最小圆的半径是 .
-
科目: 来源: 题型:
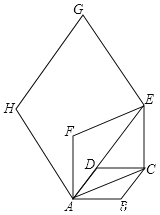
查看答案和解析>>【题目】如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第六个菱形的边长为( )
A. 9 B.
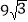 C. 27 D.
C. 27 D. 
-
科目: 来源: 题型:
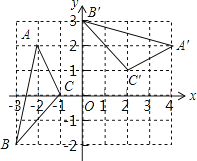
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知线段AB=12cm,点C为线段AB上的一动点,点D,E分别是AC和BC中点.
(1)若点C恰好是AB的中点,则DE=_______cm;
(2)若AC=4cm,求DE的长;
(3)试说明无论AC取何值(不超过12cm),DE的长不变;
(4)如图②,已知∠AOB=120°,过角的内部任一点C画射线OC.若OD,OE分别平分∠AOC和∠BOC.试说明∠DOE的度数与射线OC的位置无关.
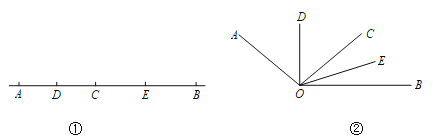
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分10分)
如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于
 BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形. (1)根据以上尺规作图的过程,求证四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=4
 ,求∠C的大小.
,求∠C的大小.
相关试题

