【题目】已知正△ABC的边长为6,那么能够完全覆盖这个正△ABC的最小圆的半径是 .
参考答案:
【答案】2 ![]()
【解析】解:如图,那么能够完全覆盖这个正△ABC的最小圆的半径就是△ABC外接圆的半径,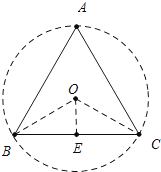
设⊙O是△ABC的外接圆,连接OB,OC,作OE⊥BC于E,
∵△ABC是等边三角形,
∴∠A=60°,∠BOC=2∠A=120°,
∵OB=OC,OE⊥BC,
∴∠BOE=60°,BE=EC=3,
∴sin60°= ![]() ,∴OB=2
,∴OB=2 ![]() ,
,
故答案为2 ![]() .
.
能够完全覆盖这个正△ABC的最小圆的半径是△ABC外接圆的半径,求出△ABC外接圆的半径即可解决问题. 本题考查等边三角形的性质、三角形外接圆的性质、锐角三角函数等知识,解题的关键是理解题意,学会转化的思想解决问题,属于中考常考题型.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小武新家装修,在装修客厅时,购进彩色地砖和单色地砖共100块,共花费5600元.已知彩色地砖的单价是80元/块,单色地砖的单价是40元/块.
(1)两种型号的地砖各采购了多少块?
(2)如果厨房也要铺设这两种型号的地砖共60块,且采购地砖的费用不超过3200元,那么彩色地砖最多能采购多少块?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△AOB中,∠AOB=90°,OA在x轴上,OB在y轴上,点A,B的坐标分别为(
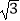 ,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为 .
,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为 . 
-
科目: 来源: 题型:
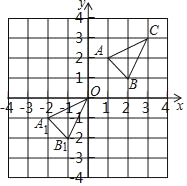
查看答案和解析>>【题目】如图,已知△ABC经过平移后得到△A1B1C1,点A与A1,点B与B1,点C与C1分别是对应点,观察各对应点坐标之间的关系,解答下列问题:
(1)分别写出点A与A1,点B与B1,点C与C1的坐标;
(2)若点P(x,y)通过上述的平移规律平移得到的对应点为Q(3,5),求p点坐标.
-
科目: 来源: 题型:
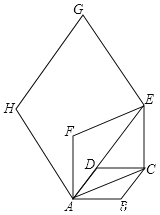
查看答案和解析>>【题目】如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第六个菱形的边长为( )
A. 9 B.
 C. 27 D.
C. 27 D. 
-
科目: 来源: 题型:
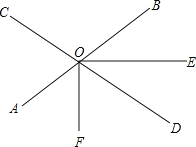
查看答案和解析>>【题目】如图,直线AB、CD相交于O点,∠AOC=70,OF平分∠AOD,射线OE在∠BOD的内部(如图),∠BOE=n°.
(1)当n=30时,求∠DOE的度数;
(2)当n=35时,射线OE与OF之间有什么位置关系?
(3)若射线OD平分∠EOF,求n的值.
-
科目: 来源: 题型:
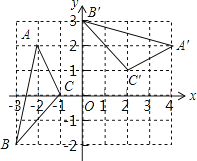
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为 .
相关试题

