【题目】如图①,已知线段AB=12cm,点C为线段AB上的一动点,点D,E分别是AC和BC中点.
(1)若点C恰好是AB的中点,则DE=_______cm;
(2)若AC=4cm,求DE的长;
(3)试说明无论AC取何值(不超过12cm),DE的长不变;
(4)如图②,已知∠AOB=120°,过角的内部任一点C画射线OC.若OD,OE分别平分∠AOC和∠BOC.试说明∠DOE的度数与射线OC的位置无关.
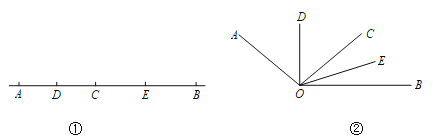
参考答案:
【答案】(1)6cm;(2)6cm;(3)理由见解析;(4)理由见解析.
【解析】试题分析:(1)由中点的定义即可解答;
(2)先求出BC的长,再由中点定义即可解答;
(3)由中点定义可得:DE=![]() AB,只与AB的长有关;
AB,只与AB的长有关;
(4)由角平分线的定义可得:∠DOE=![]() ∠AOB,即可得出结论.
∠AOB,即可得出结论.
试题解析:解:(1)∵AB=12cm,C点为AB的中点,∴AC=BC=6cm.
∵点D、E分别是AC和BC的中点,∴CD=CE=3cm,∴DE=6cm.
(2)∵AB=12cm,AC=4cm,∴BC=8cm.
∵点D、E分别是AC和BC的中点,∴CD=2cm,CE=4cm,∴DE=6cm;
(3)设AC=acm.∵点D、E分别是AC和BC的中点,∴DE=CD+CE=![]() AB=6cm,∴不论AC取何值(不超过12cm),DE的长不变;
AB=6cm,∴不论AC取何值(不超过12cm),DE的长不变;
(4)∵OD、OE分别平分∠AOC和∠BOC,∴∠DOE=∠DOC+∠COE=![]() ∠AOB.
∠AOB.
∵∠AOB=120°,∴∠DOE=60°,∴∠DOE的度数与射线OC的位置无关.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2
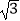 ,则阴影部分图形的面积为( )
,则阴影部分图形的面积为( ) 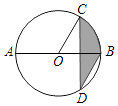
A.4π
B.2π
C.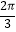
D.
-
科目: 来源: 题型:
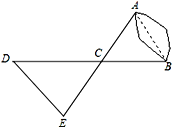
查看答案和解析>>【题目】如图,A、B两点分别位于一个池塘的两侧,池塘西边有一座假山D,在DB的中点C处有一个雕塑,小川从点A出发,沿直线AC一直向前经过点C走到点E,并使CE=CA,然后他测量点E到假山D的距离,则DE的长度就是A、B两点之间的距离.
(1)你能说明小川这样做的根据吗?
(2)如果小川恰好未带测量工具,但是知道A和假山D、雕塑C分别相距200米、120米,你能帮助他确定AB的长度范围吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
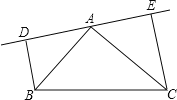
(2)若B、C在DE的两侧(如图所示),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.

-
科目: 来源: 题型:
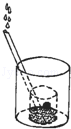
查看答案和解析>>【题目】一个大烧杯中装有一个小烧杯,在小烧杯中放入一个浮子(质量非常轻的空心小圆球)后再往小烧杯中注水,水流的速度恒定不变,小烧杯被注满后水溢出到大烧杯中,浮子始终保持在容器的正中间.用x表示注水时间,用y表示浮子的高度,则用来表示y与x之间关系的选项是( )
A.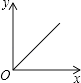
B.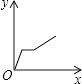
C.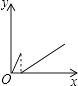
D.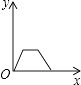
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:
①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=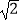 .
.
其中正确的结论有( )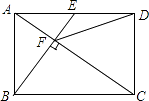
A.4个
B.3个
C.2个
D.1个
相关试题

