【题目】(本小题满分10分)
如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)根据以上尺规作图的过程,求证四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=4![]() ,求∠C的大小.
,求∠C的大小.

参考答案:
【答案】(1)详见解析;(2)60°.
【解析】
试题分析:(1)由作图过程可知,AB=AF,AE平分∠BAD,即可得∠BAE=∠EAF.再由四边形ABCD为平行四边形,可得BC∥AD,根据平行线的性质可得∠AEB=∠EAF,所以∠BAE=∠AEB,根据等腰三角形的性质可得AB=BE,即可得BE=AF,所以四边形ABEF为平行四边形,根据一组邻边相等的平行四边形是菱形即可判定四边形ABEF为菱形;(2)连接BF,已知四边形ABEF为菱形,根据菱形的性质可得BF与AE互相垂直平分,∠BAE=∠FAE,OA=![]() AE=
AE=![]() .再由菱形ABEF的周长为16,可得AF=4.所以cos∠OAF=
.再由菱形ABEF的周长为16,可得AF=4.所以cos∠OAF=![]() =
=![]() .即可得∠OAF=30°,所以∠BAF=60°.再由平行线的性质即可得∠C=∠BAD=60°.
.即可得∠OAF=30°,所以∠BAF=60°.再由平行线的性质即可得∠C=∠BAD=60°.
试题解析:
(1)由作图过程可知,AB=AF,AE平分∠BAD.∴∠BAE=∠EAF.
∵四边形ABCD为平行四边形,∴BC∥AD.∴∠AEB=∠EAF.
∴∠BAE=∠AEB,∴AB=BE.∴BE=AF.∴四边形ABEF为平行四边形.
∴四边形ABEF为菱形.
(2)连接BF,
![]()
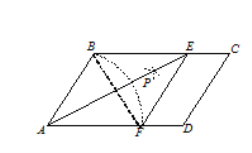
∵四边形ABEF为菱形,∴BF与AE互相垂直平分,∠BAE=∠FAE.
∴OA=![]() AE=
AE=![]() .∵菱形ABEF的周长为16,∴AF=4.
.∵菱形ABEF的周长为16,∴AF=4.
∴cos∠OAF=![]() =
=![]() .∴∠OAF=30°,∴∠BAF=60°.
.∴∠OAF=30°,∴∠BAF=60°.
∵四边形ABCD为平行四边形,∴∠C=∠BAD=60°.
-
科目: 来源: 题型:
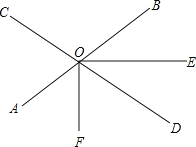
查看答案和解析>>【题目】如图,直线AB、CD相交于O点,∠AOC=70,OF平分∠AOD,射线OE在∠BOD的内部(如图),∠BOE=n°.
(1)当n=30时,求∠DOE的度数;
(2)当n=35时,射线OE与OF之间有什么位置关系?
(3)若射线OD平分∠EOF,求n的值.
-
科目: 来源: 题型:
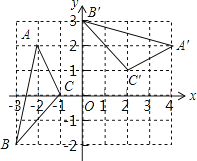
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知线段AB=12cm,点C为线段AB上的一动点,点D,E分别是AC和BC中点.
(1)若点C恰好是AB的中点,则DE=_______cm;
(2)若AC=4cm,求DE的长;
(3)试说明无论AC取何值(不超过12cm),DE的长不变;
(4)如图②,已知∠AOB=120°,过角的内部任一点C画射线OC.若OD,OE分别平分∠AOC和∠BOC.试说明∠DOE的度数与射线OC的位置无关.
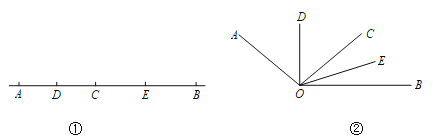
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生的体能情况,随机选取了1000名学生进行调查,并记录了他们对长跑、短跑、跳绳、跳远四个项目的喜欢情况,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.
项目
学生长跑
短跑
跳绳
跳远
200
√
×
√
√
300
×
√
×
√
150
√
√
√
×
200
√
×
√
×
150
√
×
×
×
(1)估计学生同时喜欢短跑和跳绳的概率;
(2)估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
(3)如果学生喜欢长跑、则该同学同时喜欢短跑、跳绳、跳远中哪项的可能性大? -
科目: 来源: 题型:
查看答案和解析>>【题目】在等边△ABC中,点D,E分别在边BC、AC上,若CD=2,过点D作DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,求EF的长.
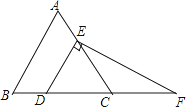
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.
(1)求每行驶1千米纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?
相关试题

