搜索
【题目】如图，二次函数y= 
x2（0≤x≤2）的图象记为曲线C1 ， 将C1绕坐标原点O逆时针旋转90°，得曲线C2 ．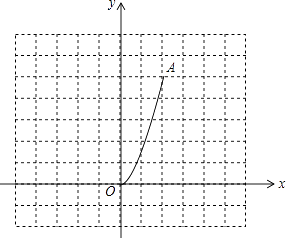 
（1）请画出C2；
（2）写出旋转后A（2，5）的对应点A1的坐标；
（3）直接写出C1旋转至C2过程中扫过的面积 ．
参考答案：
【答案】
（1）解：如图，曲线C2即为所求
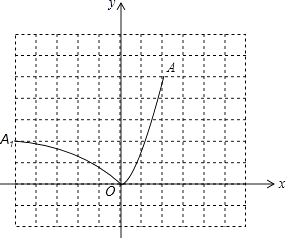
（2）（﹣5，2）
（3）
π
【解析】解：（2）由图可知，A1（﹣5，2）． 所以答案是：（﹣5，2）；（3）∵OA= 
= 
，
∴C1旋转至C2过程中扫过的面积= 
= π．
所以答案是： π．
【考点精析】认真审题，首先需要了解二次函数图象的平移(平移步骤：（1）配方 y=a(x-h)2+k，确定顶点（h,k）（2）对x轴左加右减；对y轴上加下减)，还要掌握扇形面积计算公式(在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）)的相关知识才是答题的关键．
-
科目： 来源： 题型：
查看答案和解析>>【题目】直线y=m是平行于x轴的直线，将抛物线y=﹣
x2﹣4x在直线y=m上侧的部分沿直线y=m翻折，翻折后的部分与没有翻折的部分组成新的函数图象，若新的函数图象刚好与直线y=﹣x有3个交点，则满足条件的m的值为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法中错误的是( )
A. 在△ABC中，∠C＝∠A－∠B，则△ABC为直角三角形
B. 在△ABC中，若∠A∶∠B∶∠C＝5∶2∶3，则△ABC为直角三角形
C. 在△ABC中，若a＝
c，b＝
c，则△ABC为直角三角形D. 在△ABC中，若a∶b∶c＝2∶2∶4，则△ABC为直角三角形
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB为⊙O的直径，弦CD⊥AB于E，∠CDB=15°，OE=2
． 
（1）求⊙O的半径；
（2）将△OBD绕O点旋转，使弦BD的一个端点与弦AC的一个端点重合，则弦BD与弦AC的夹角为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，D为Rt△ABC斜边AB上一点，以CD为直径的圆分别交△ABC三边于E、F、G三点，连接FE，FG．
（1）求证：∠EFG=∠B；
（2）若AC=2BC=4
，D为AE的中点，求FG的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】为了美化环境，学校准备在如图所示的矩形ABCD空地上进行绿化，规划在中间的一块四边形MNQP上种花，其余的四块三角形上铺设草坪，要求AM=AN=CP=CQ，已知BC=24米，AB=40米，设AN=x米，种花的面积为y1平方米，草坪面积y2平方米．
（1）分别求y1和y2与x之间的函数关系式（不要求写出自变量的取值范围）；
（2）当AN的长为多少米时，种花的面积为440平方米？
（3）若种花每平方米需200元，铺设草坪每平方米需100元，现设计要求种花的面积不大于440平方米，设学校所需费用W（元），求W与x之间的函数关系式，并求出学校所需费用的最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2+2ax+c的图象与x轴交于A、B两点（点A在点B的左边）AB=4，与y轴交于点C，OC=OA，点D为抛物线的顶点．
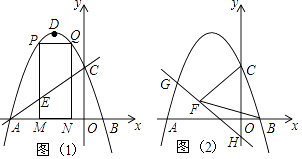
（1）求抛物线的解析式；
（2）点M（m，0）为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，可得矩形PQNM，如图1，点P在点Q左边，当矩形PQNM的周长最大时，求m的值，并求出此时的△AEM的面积；
（3）已知H（0，﹣1），点G在抛物线上，连HG，直线HG⊥CF，垂足为F，若BF=BC，求点G的坐标．
相关试题
