【题目】如图,D为Rt△ABC斜边AB上一点,以CD为直径的圆分别交△ABC三边于E、F、G三点,连接FE,FG. 
(1)求证:∠EFG=∠B;
(2)若AC=2BC=4 ![]() ,D为AE的中点,求FG的长.
,D为AE的中点,求FG的长.
参考答案:
【答案】
(1)证明:连接EC,如图1所示.
∵CD为直径,
∴∠AEC=90°,
∴∠BCE+∠B=90°.
∵∠BCE+∠ECA=90°,
∴∠B=∠ECA.
又∵∠ECA=∠EFG,
∴∠EFG=∠B
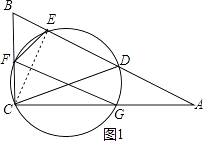
(2)解:在Rt△BCA中,AC=4 ![]() ,BC=2
,BC=2 ![]() ,
,
∴AB= ![]() =10.
=10.
∵BCAC=ABCE,
∴CE=4.
∵tan∠A= ![]() =
= ![]() =
= ![]() ,
,
∴AE=2CE=8.
在Rt△DCG中,CE=4,ED= ![]() AE=4,
AE=4,
∴CD= ![]() =4
=4 ![]() .
.
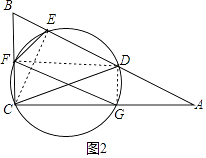
连接FD、DG,如图2所示.
∵CD是直径,
∴∠CFD=∠CGD=90°,
又∵∠FCG=90°,
∴四边形FCGD为矩形,
∴FG=CD=4 ![]() .
.
【解析】(1)连接EC,则∠AEC=90°,由同角的余角相等即可得出∠B=∠ECA,再根据圆周角定理即可得出∠ECA=∠EFG,由此即可证出∠EFG=∠B;(2)由AC、BC的长度利用勾股定理即可求出AB的长度,结合面积法即可得出CE的长度,由正切即可得出AE的长度,再利用勾股定理可求出CD的长度,连接FD、DG,由矩形的判定定理即可证出四边形FCGD为矩形,利用矩形的性质即可得出FG=CD,此题得解.
【考点精析】本题主要考查了勾股定理的概念和圆周角定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中错误的是( )
A. 在△ABC中,∠C=∠A-∠B,则△ABC为直角三角形
B. 在△ABC中,若∠A∶∠B∶∠C=5∶2∶3,则△ABC为直角三角形
C. 在△ABC中,若a=
 c,b=
c,b= c,则△ABC为直角三角形
c,则△ABC为直角三角形D. 在△ABC中,若a∶b∶c=2∶2∶4,则△ABC为直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,弦CD⊥AB于E,∠CDB=15°,OE=2
 .
. 
(1)求⊙O的半径;
(2)将△OBD绕O点旋转,使弦BD的一个端点与弦AC的一个端点重合,则弦BD与弦AC的夹角为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=
 x2(0≤x≤2)的图象记为曲线C1 , 将C1绕坐标原点O逆时针旋转90°,得曲线C2 .
x2(0≤x≤2)的图象记为曲线C1 , 将C1绕坐标原点O逆时针旋转90°,得曲线C2 . 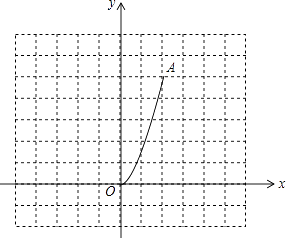
(1)请画出C2;
(2)写出旋转后A(2,5)的对应点A1的坐标;
(3)直接写出C1旋转至C2过程中扫过的面积 . -
科目: 来源: 题型:
查看答案和解析>>【题目】为了美化环境,学校准备在如图所示的矩形ABCD空地上进行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ,已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.

(1)分别求y1和y2与x之间的函数关系式(不要求写出自变量的取值范围);
(2)当AN的长为多少米时,种花的面积为440平方米?
(3)若种花每平方米需200元,铺设草坪每平方米需100元,现设计要求种花的面积不大于440平方米,设学校所需费用W(元),求W与x之间的函数关系式,并求出学校所需费用的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+2ax+c的图象与x轴交于A、B两点(点A在点B的左边)AB=4,与y轴交于点C,OC=OA,点D为抛物线的顶点.
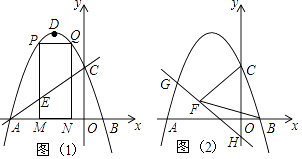
(1)求抛物线的解析式;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM,如图1,点P在点Q左边,当矩形PQNM的周长最大时,求m的值,并求出此时的△AEM的面积;
(3)已知H(0,﹣1),点G在抛物线上,连HG,直线HG⊥CF,垂足为F,若BF=BC,求点G的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=ax+b与y=ax2﹣bx的图象可能是( )
A.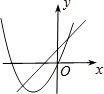
B.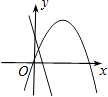
C.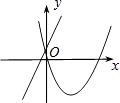
D.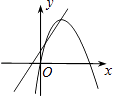
相关试题

