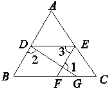
【题目】如图所示,已知点D,E分别在AB,AC上,EF交BC于点F,DG交BC于点G,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并说明理由.
参考答案:
【答案】见解析
【解析】
根据∠1=∠ADG,得出∠3=∠ADE,又因为∠B=∠3,所以∠ADE=∠B,再利用同位角相等,两直线平行证明DE∥BC,最后可得∠AED与∠C的大小关系.
∠AED=∠C.
理由:因为∠2+∠ADG=180°(邻补角定义),
∠1+∠2=180°(已知),
所以∠1=∠ADG(同角的补角相等),
所以EF∥AB(同位角相等,两直线平行),
所以∠3=∠ADE(两直线平行,内错角相等).
又因为∠B=∠3(已知),
所以∠ADE=∠B(等量代换),
所以DE∥BC(同位角相等,两直线平行),
所以∠AED=∠C(两直线平行,同位角相等).
-
科目: 来源: 题型:
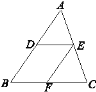
查看答案和解析>>【题目】如图,点D,E分别在AB,AC上,DE∥BC,EF平分∠DEC,交BC于点F,且∠ABC=55°,∠C=70°.
(1)求∠DEF的度数;
(2)请判断EF与AB的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1和∠2互补,∠C=∠EDF.
(1)判断DF与EC的关系为 .
(2)试判断DE与BC的关系,并说明理由.
(3)试判断∠DEC与∠DFC的关系并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题7分)如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.
(1)判断线段AB与DE的数量关系和位置关系,并说明理由;
(2)连接BD、BE,若设BC=a,AC=b,AB=c,请利用四边形ADBE的面积证明勾股定理.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是BC边上的一点,∠B=44°,∠BAD=28°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠AFC= 度;
(2)求∠EDF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如: 2⊕5=2(2-5)+1=2(-3)+1=-6+1=-5.
(1)求(-2)⊕3的值
(2)若3⊕x的值小于13,求x的取值范围,并在图示的数轴上表示出来.
相关试题

