【题目】如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)
参考答案:
【答案】解:作BG⊥AC于G,
∵点C在A的南偏东60°,
∴∠A=90°﹣60°=30°,
∵C在B的南偏东30°,
∴∠ABC=120°,
∴∠C=30°,
∴BC=AB=100里,
∴BG=BCsin30°=50里,
CG=BCcos30°=50![]() 里,
里,
∴AC=2CG=100![]() 里.
里.
答:A船到达事发地点C的距离是100![]() 里,B船到达事发地点C的距离是100里.
里,B船到达事发地点C的距离是100里.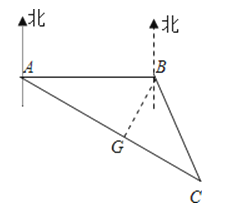
【解析】作BG⊥AC于G,在图中标注方向角,根据等腰三角形的性质和正弦、余弦的概念求出AC、BC即可.
-
科目: 来源: 题型:
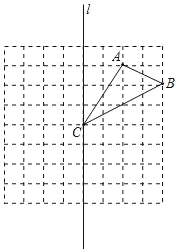
查看答案和解析>>【题目】在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点).
(1)△ABC的面积为 ;
(2)在直线l上找一点P,使点P到边AB、BC的距离相等.
(3)画出△ABC关于直线l对称的图形△A1B1C1;再将△A1B1C1向下平移4个单位,画出平移后得到的△A2B2C2.
(4)结合轴对称变换和平移变换的有关性质,两个对应三角形△ABC和△A2B2C2的对应点所具有的性质是( ).
A.对应点连线与对称轴垂直 B.对应点连线被对称轴平分或与对称轴重合
C.对应点连线被对称轴垂直平分 D.对应点连线互相平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有甲,乙两个三角形,请你用一条直线把每一个三角形分成两个等腰三角形,并标出每个三角形各角的度数.

-
科目: 来源: 题型:
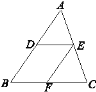
查看答案和解析>>【题目】如图,点D,E分别在AB,AC上,DE∥BC,EF平分∠DEC,交BC于点F,且∠ABC=55°,∠C=70°.
(1)求∠DEF的度数;
(2)请判断EF与AB的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1和∠2互补,∠C=∠EDF.
(1)判断DF与EC的关系为 .
(2)试判断DE与BC的关系,并说明理由.
(3)试判断∠DEC与∠DFC的关系并说明理由.

-
科目: 来源: 题型:
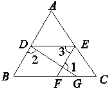
查看答案和解析>>【题目】如图所示,已知点D,E分别在AB,AC上,EF交BC于点F,DG交BC于点G,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题7分)如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.
(1)判断线段AB与DE的数量关系和位置关系,并说明理由;
(2)连接BD、BE,若设BC=a,AC=b,AB=c,请利用四边形ADBE的面积证明勾股定理.

相关试题

