【题目】定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如: 2⊕5=2(2-5)+1=2(-3)+1=-6+1=-5.
(1)求(-2)⊕3的值
(2)若3⊕x的值小于13,求x的取值范围,并在图示的数轴上表示出来.
![]()
参考答案:
【答案】(1)11
(2)x>-1。
数轴表示如图所示:
![]()
【解析】
(1)按照定义新运算a⊕b=a(a-b)+1,求解即可。
(2)先按照定义新运算a⊕b=a(a-b)+1,得出3⊕x,再令其小于13,得到一元一次不等式,解不等式求出x的取值范围,即可在数轴上表示。
不等式的解集在数轴上表示的方法:>,≥向右画;<,≤向左画,在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示。
解:(1)∵a⊕b=a(a-b)+1,
∴(-2)⊕3=-2(-2-3)+1=10+1=11。
(2)∵3⊕x<13,
∴3(3-x)+113,
9-3x+1<13,
-3x<3,
∴x>-1。
数轴表示如图所示:
![]()
-
科目: 来源: 题型:
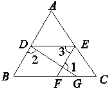
查看答案和解析>>【题目】如图所示,已知点D,E分别在AB,AC上,EF交BC于点F,DG交BC于点G,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题7分)如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.
(1)判断线段AB与DE的数量关系和位置关系,并说明理由;
(2)连接BD、BE,若设BC=a,AC=b,AB=c,请利用四边形ADBE的面积证明勾股定理.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是BC边上的一点,∠B=44°,∠BAD=28°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠AFC= 度;
(2)求∠EDF的度数.

-
科目: 来源: 题型:
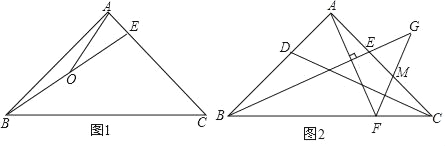
查看答案和解析>>【题目】在△ABC中,已知AB=AC,∠BAC=90°,E为边AC上一点,连接BE.
(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;
(2)如图2,D为AB上一点,且满足AE=AD,过点A作AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M,求证:BG=AF+FG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条高速公路在城市A的东偏北30°方向直线延伸,县城M在城市A东偏北60°方向上,测验员从A沿高速公路前行4000米到达C,测得县城M位于C的北偏西60°方向上,现要设计一条从县城M进入高速公路的路线,请在高速公路上寻找连接点N,使修建到县城M的道路最短,试确定N点的位置并求出最短路线长.(结果取整数,
 ≈1.732)
≈1.732)
-
科目: 来源: 题型:
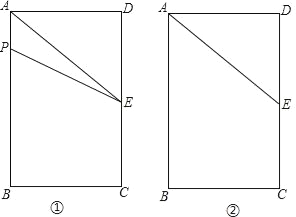
查看答案和解析>>【题目】如图①,长方形ABCD中,AB=6cm,BC=4cm,E为CD的中点.点P从A点出发,沿A﹣B﹣C的方向在长方形边上匀速运动,速度为1cm/s,运动到C点停止.设点P运动的时间为ts.(图②为备用图)
(1)当P在AB上,t= s时,△APE的面积为长方形面积的
 ;
;(2)整个运动过程中,t为何值时,△APE为直角三角形?
相关试题

