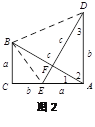
【题目】(本题7分)如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.
(1)判断线段AB与DE的数量关系和位置关系,并说明理由;
(2)连接BD、BE,若设BC=a,AC=b,AB=c,请利用四边形ADBE的面积证明勾股定理.

参考答案:
【答案】(1)AB=DE,AB⊥DE.理由见解析;(2)证明见解析.
【解析】试题分析:(1)根据垂直的定义可证得∠DAE=∠ACB=90°,然后根据ASA可证△ABC≌△DEA,从而得证AB=DE,且∠3=∠1,然后根据直角三角形的内角和等量代换可证得AB⊥DE;
(2)根据三角形的面积和四边形的面积,可知S四边形ADBE= S△ADE+ S△BDE,S四边形ADBE=S△ABE+S△ADB=![]() a2+
a2+![]() b2可得证符合勾股定理的逆定理.
b2可得证符合勾股定理的逆定理.
试题解析:(1)解:AB=DE, AB⊥DE.
如图2,∵AD⊥CA,∴∠DAE=∠ACB=90°,
∵AE=BC,∠DAE=∠ACB,AD=AC,∴△ABC≌△DEA,∴AB=DE,
∠3=∠1,∵∠DAE=90°,∴∠1+∠2=90°,∴∠3+∠2=90°,
∴∠AFE=90°,∴AB⊥DE.
(2)如图2,∵S四边形ADBE= S△ADE+ S△BDE=![]() DE·AF+
DE·AF+![]() DE·BF=
DE·BF=![]() DE·AB =
DE·AB =![]() c2,
c2,
S四边形ADBE=S△ABE+S△ADB=![]() a2+
a2+![]() b2,
b2,
∴![]() a2+
a2+![]() b2=
b2=![]() c2,∴a2+b2=c2.
c2,∴a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣1)2018﹣|﹣2|+3×(﹣2)+2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD(四边相等,四个角都是直角)的边长为4,点P从点A出发,以每秒1个单位长度的速度沿射线AD向点D运动;点Q从点D同时出发,以相同的速度沿射线AD方向向右运动,当点P到达点D时,点Q也停止运动,连接BP,过点P作BP的垂线交过点Q平行于CD的直线l于点E,BE于CD相交于点F,连接PF,设点P运动时间为t(s),
(1)求∠PBE的度数;
(2)当t为何值时,△PQF是以PF为腰的等腰三角形?
(3)试探索在运动过程中△PDF的周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果阳光斜射在地面上,一张矩形纸片在地面上的影子不可能是( )
A.矩形
B.线段
C.平行四边形
D.一个点 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明在大楼45米高(即PH=45米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:
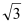 ,点P、H、B、C、A在同一个平面上,点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上,点H、B、C在同一条直线上,且PH⊥HC.(1)山坡坡脚(即∠ABC)的度数等于 度;
(2)求A、B两点间的距离.(结果精确到1米,参考数据:
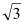 ≈1.732)
≈1.732)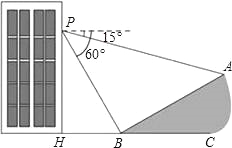
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:2(x2-2xy)-3(-xy-x2)-xy,其中x,y满足|x+1|+(y-2)2=0
-
科目: 来源: 题型:
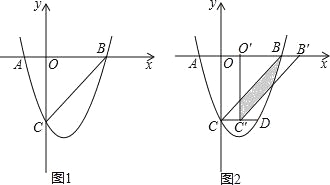
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴、y轴分别交于点A(﹣1,0),B(3,0)、C(0,﹣3)三点.
(1)直接写出抛物线的解析式 ;
(2)点D(2,m)在第一象限的抛物线上,连接BC、BD,试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标;如果不存在,请说明理由.
(3)如图2,在(2)的条件下,将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B′O′C′,在平移过程中,△B′O′C′与△BCD重叠的面积记为S,设平移的时间为t秒(0≤t≤3),试求S与t之间的函数关系式?
相关试题

