Question

【题目】如图，抛物线y=﹣x2+（m﹣1）x+m（m＞1）与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C（0，3）．

（1）求抛物线的解析式；
（2）点D和点C关于抛物线的对称轴对称，点你F在直线AD上方的抛物线上，FG⊥AD于G，FH∥x轴交直线AD于H，求△FGH的周长的最大值；
（3）点M是抛物线的顶点，直线l垂直于直线AM，与坐标轴交于P、Q两点，点R在抛物线的对称轴上，使得△PQR是以PQ为斜边的等腰直角三角形，求直线l的解析式．

Answer 1

【答案】
（1）

解：把C（0，3）代入y=﹣x2+（m﹣1）x+m得m=3，

∴抛物线的解析式为：y=﹣x2+2x+3，

（2）

解：令y=﹣x2+2x+3=0，解得：x1=﹣1，x2=3，∴A（﹣1，0），B（3，0），C（0，3），

∵点D和点C关于抛物线的对称轴对称，

∴D（1，2），AD的解析式y=x+1，

∴OA=OE=1，

∴∠EAO=45°，

∵FH∥AB，

∴∠FHA=∠EAO=45°，

∵FG⊥AH，

∴△FGH是等腰直角三角形，

设点F坐标（m，﹣m2+2m+3），

∴点H坐标（﹣m2+2m+2，﹣m2+2m+3），

∴FH=﹣m2+m+2，

∴△FGH的周长=（﹣m2+m+2）+2× （﹣m2+m+2）=﹣（1+ ）（m﹣ ）2+

∴△FGH的周长最大值为 ；

（3）

解：∵抛物线y=﹣x2+2x+3的定点坐标为（1，4），

∴直线AM的解析式为y=2x+2，

∵直线l垂直于直线AM，

∴设直线l的解析式为y=﹣ x+b，

∵与坐标轴交于P、Q两点，

∴直线l的解析式为y=﹣ x+b与y轴的交点P（0，b），与x轴的交点Q（2b，0），

设R（1，a），

∴PR2=（﹣1）2+（a﹣b）2，QR2=（2b﹣1）2+a2，PQ2=b2+（2b）2=5b2，

∵△PQR是以PQ为斜边的等腰直角三角形，

∴PR2=QR2，即（﹣1）2+（a﹣b）2=QR2=（2b﹣1）2+a2，

∴﹣2a=3b﹣4，①

∴PR2+QR2=PQ2，

即（﹣1）2+（a﹣b）2+（2b﹣1）2+a2=5b2，

∴2a2﹣2ab﹣4b+2=0，②

联立①②解得： ， ，

∴直线l的解析式为y=﹣ x+ 或y=﹣ x+2．

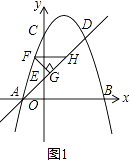
【解析】（1）求出A、D两点坐标，利用待定系数法即可解决问题．（2）首先证明△FHG是等腰直角三角形，构建二次函数利用函数性质解决问题即可；（3）求得直线AM的解析式为y=2x+2，根据直线l垂直于直线AM，设直线l的解析式为y=﹣ x+b，得到直线l的解析式为y=﹣ x+b与y轴的交点P（0，b），与x轴的交点Q（2b，0），设R（1，a），根据勾股定理列方程即可得到结论．
【考点精析】关于本题考查的二次函数的性质，需要了解增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能得出正确答案．