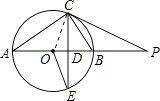
【题目】如图,已知,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点,连结OE,AC,且∠P=∠E,∠POE=2∠CAB. 
(1)求证:CE⊥AB;
(2)求证:PC是⊙O的切线;
(3)若BD=2OD,且PB=9,求⊙O的半径长和tan∠P的值.
参考答案:
【答案】
(1)证明:连接OC,
∴∠COB=2∠CAB,
又∠POE=2∠CAB.
∴∠COD=∠EOD,
又∵OC=OE,
∴∠ODC=∠ODE=90°,
即CE⊥AB;
(2)证明:证明:∵CE⊥AB,∠P=∠E,
∴∠P+∠PCD=∠E+∠PCD=90°,
又∠OCD=∠E,
∴∠OCD+∠PCD=∠PCO=90°,
∴PC是⊙O的切线;
(3)解:设⊙O的半径为r,OD=x,则BD=2x,r=3x,
∵CD⊥OP,OC⊥PC,
∴Rt△OCD∽Rt△OPC,
∴OC2=ODOP,即(3x)2=x(3x+9),
解之得x= ![]() ,
,
∴⊙O的半径r= ![]() ,
,
同理可得PC2=PDPO=(PB+BD)(PB+OB)=162,
∴PC=9 ![]() ,
,
在Rt△OCP中,tan∠P= ![]() =
= ![]() .
.
【解析】(1)只要证明∠DOC=∠DOE,利用等腰三角形的三线合一即可证明;(2)欲证明PC是⊙O的切线,只要证明∠OCP=90°即可;(3)设⊙O的半径为r,OD=x,则BD=2x,r=3x,易证得Rt△OCD∽Rt△OPC,根据相似三角形的性质得OC2=ODOP,即(3x)2=x(3x+9),解出x,即可得圆的半径;同理可得PC2=PDPO=(PB+BD)(PB+OB)=162,可计算出PC,然后在Rt△OCP中,根据正切的定义即可得到tan∠P的值.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:
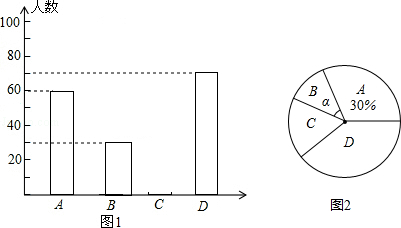
(1)本次抽样调查共抽取了多少名学生?并将条形统计图补充完整;
(2)本次抽样调查中,学习时间的中位数落在哪个等级内?
(3)表示B等级的扇形圆心角α的度数是多少?
(4)在此次问卷调查中,甲班有2人平均每天课外学习时间超过2小时,乙班有3人平均每天课外学习时间超过2小时,若从这5人中任选2人去参加座谈,试用列表或化树状图的方法求选出的2人来自不同班级的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.

(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,地面上两个村庄C、D处于同一水平线上,一飞行器在空中以6千米/小时的速度沿MN方向水平飞行,航线MN与C、D在同一铅直平面内.当该飞行器飞行至村庄C的正上方A处时,测得∠NAD=60°;该飞行器从A处飞行40分钟至B处时,测得∠ABD=75°.求村庄C、D间的距离(
 取1.73,结果精确到0.1千米)
取1.73,结果精确到0.1千米) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+(m﹣1)x+m(m>1)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C(0,3).

(1)求抛物线的解析式;
(2)点D和点C关于抛物线的对称轴对称,点你F在直线AD上方的抛物线上,FG⊥AD于G,FH∥x轴交直线AD于H,求△FGH的周长的最大值;
(3)点M是抛物线的顶点,直线l垂直于直线AM,与坐标轴交于P、Q两点,点R在抛物线的对称轴上,使得△PQR是以PQ为斜边的等腰直角三角形,求直线l的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,把两个全等的三角板ABC、EFG叠放在一起,使三角板EFG的直角边FG经过三角板ABC的直角顶点C,垂直AB于G,其中∠B=∠F=30°,斜边AB和EF均为4.现将三角板EFG由图1所示的位置绕G点沿逆时针方向旋转α(0°<α<90°),如图2,EG交AC于点K,GF交BC于点H.在旋转过程中,请你解决以下问题:

(1)求证:△CGH∽△AGK;
(2)连接HK,求证:KH∥EF;
(3)设AK=x,△CKH的面积为y,求y关于x的函数关系式,并求出y的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为⊙O的内接四边形,且对角线AC为直径,AD=BC,过点D作DG⊥AC,垂足为E,DG分别与AB及CB延长线交于点F、M.

(1)求证:四边形ABCD是矩形;
(2)若点G为MF的中点,求证:BG是⊙O的切线;
(3)若AD=4,CM=9,求四边形ABCD的面积.
相关试题

