【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
参考答案:
【答案】![]()
【解析】试题分析:先利用树状图展示所有9种等可能的结果数,即组成的两位数为33,34,35,43,44,45,53,54,55;其中十位上的数字与个位上的数字之和为9的两位数有45和54两个,然后根据概率的概念计算即可.
试题解析:画树状图如下:
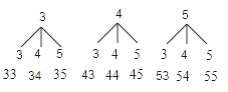
共有9种等可能的结果数,即按这种方法能组成的两位数有33,34,35,43,44,45,53,54,55;
其中十位上的数字与个位上的数字之和为9的两位数有45和54两个,
∴P(十位与个位数字之和为9)=![]() .
.
-
科目: 来源: 题型:
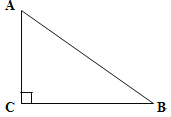
查看答案和解析>>【题目】如图,已知△ABC,∠C=90,AC<BC,D为BC上一点,且到A,B两点的距离相等.
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=37°,则∠CAD=_________度.
-
科目: 来源: 题型:
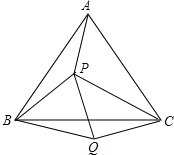
查看答案和解析>>【题目】如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(1) 观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2) 若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)图(1)是一个长为2m,宽为2n的矩形,把此矩形沿图中虚线用剪刀均分为四个小长方形,然后按图(2)的形状拼成一个大正方形.请问:这两个图形的什么量不变?
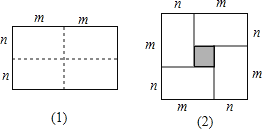
(2)把所得的大正方形面积比原矩形的面积多出的阴影部分的面积用含m,n的代数式表示为(m-n)2或m2-2mn+n2 .
(3)由前面的探索可得出的结论是:在周长一定的矩形中,当 时,面积最大.
(4)若矩形的周长为24cm,则当边长为多少时,该图形的面积最大?最大面积是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)23-17-(-7)+(-16);
(2)

(3)
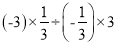
(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=90°,D是BC边上任意一点,求证:BD
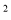 +CD
+CD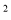 =2AD
=2AD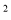 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC交BC于点E,D为AC上的点,BE=DE.
(1)求证:∠B+∠EDA=180°;
(2)求
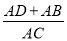 的值。.
的值。.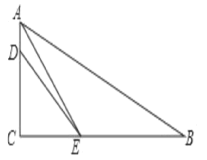
相关试题

