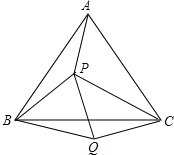
【题目】如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(1) 观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2) 若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状,并说明理由.
参考答案:
【答案】(1)AP=CQ,证明见解析(2)△PQC是直角三角形,证明见解析
【解析】
根据等边三角形的性质利用SAS判定△ABP≌△CBQ,从而得到AP=CQ;设PA=3a,PB=4a,PC=5a,由已知可判定△PBQ为正三角形从而可得到PQ=4a,再根据勾股定理判定△PQC是直角三角形.
(1)猜想:AP=CQ,
证明:∵∠ABP+∠PBC=60°,∠QBC+∠PBC=60°,
∴∠ABP=∠QBC.
又AB=BC,BP=BQ,
∴△ABP≌△CBQ,
∴AP=CQ;
(2)由PA:PB:PC=3:4:5,
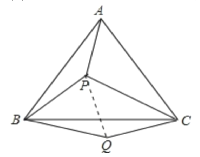
可设PA=3a,PB=4a,PC=5a,
连接PQ,在△PBQ中
由于PB=BQ=4a,且∠PBQ=60°,
∴△PBQ为正三角形.
∴PQ=4a.
于是在△PQC中
∵PQ![]() +QC
+QC![]() =16a
=16a![]() +9a
+9a![]() =25a
=25a![]() =PC
=PC![]()
∴△PQC是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现用a根长度相同的火柴棒,按如图①摆放时可摆成m个正方形,按如图②摆放时可摆放2n个正方形.

(1)如图①,当m=2时,a= ,如图②,当n=3时,a= ;
(2) m与n之间有何数量关系,请你写出来并说明理由;
(3)现有56根火柴棒,现用若干根火柴棒摆成图①的形状后,剩下的火柴棒刚好可以摆成图②的形状。请你直接写出一种摆放方法,并通过计算验证你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
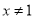 ,
,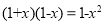
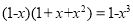
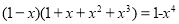
请按规律,进行以下的探索:
①

②

③

求
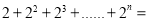 . (用含n的代数式表示)
. (用含n的代数式表示) -
科目: 来源: 题型:
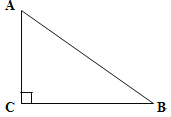
查看答案和解析>>【题目】如图,已知△ABC,∠C=90,AC<BC,D为BC上一点,且到A,B两点的距离相等.
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=37°,则∠CAD=_________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)图(1)是一个长为2m,宽为2n的矩形,把此矩形沿图中虚线用剪刀均分为四个小长方形,然后按图(2)的形状拼成一个大正方形.请问:这两个图形的什么量不变?
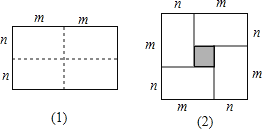
(2)把所得的大正方形面积比原矩形的面积多出的阴影部分的面积用含m,n的代数式表示为(m-n)2或m2-2mn+n2 .
(3)由前面的探索可得出的结论是:在周长一定的矩形中,当 时,面积最大.
(4)若矩形的周长为24cm,则当边长为多少时,该图形的面积最大?最大面积是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)23-17-(-7)+(-16);
(2)

(3)
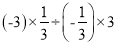
(4)

相关试题

